雑音指数測定の重要性
2つのステージで構成される2ポート・ネットワークを考えます。最初のステージにはその入力に熱雑音が存在します。この熱雑音は最初のステージのゲインによって増幅され、最初のステージによって生成された任意の相加性雑音がそれに加えられます。そうすると、最初のステージの出力での雑音は次のようになります。

2番目のステージでは、最初の出力がその入力として提示されます。2番目のステージは入力を増幅し、さらなる相加性雑音を寄与します。
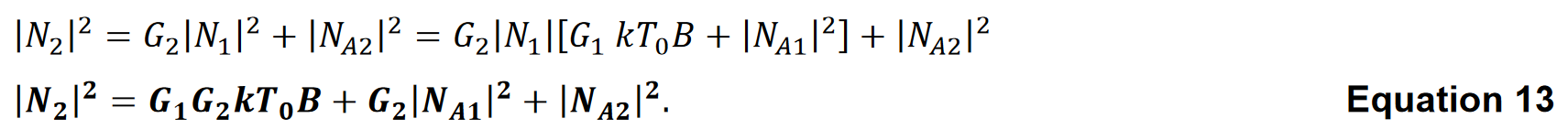
上述した原理は、複数のステージに拡張することができます。
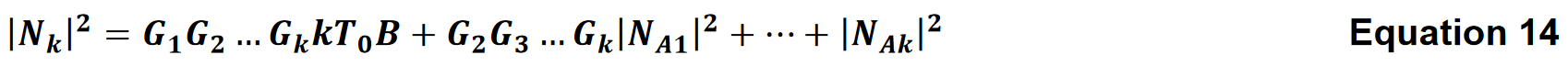
雑音指数(真値)は、入力での信号対雑音比(SNR)と出力での信号対雑音比の比です。与えられた入力信号に対して、k ステージのカスケードの比は次の通りです。

方程式6を方程式16に適用すると、 k ステージのカスケードから成るシステムの雑音指数(dB)計算が得られます。システム内のKステージを考えます。k 番目のステージは電力ゲイン GK と雑音指数 Fk を持っています。前のステージからの信号と雑音は k 番目のステージの入力に到達します。k 番目のステージの寄与は、それに先行するゲインによって減少します。Kステージのカスケードの雑音指数(dB)計算は以下から求めることができます。
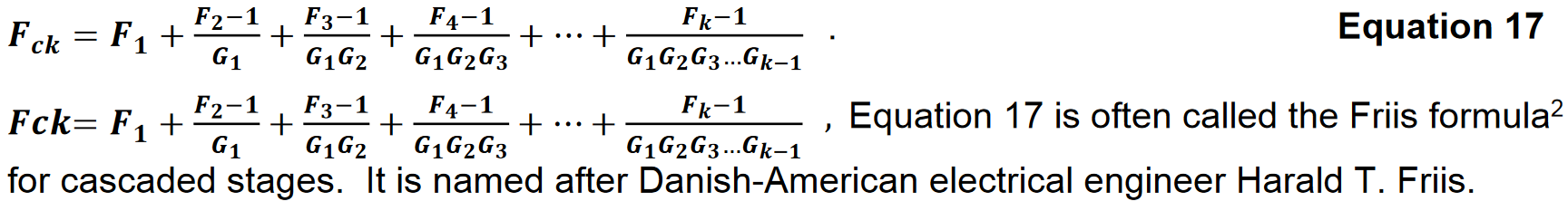
カスケード・ステージの実効雑音温度
同じ方程式を操作して、カスケード・ステージの実効雑音温度を求めることができます。各ステージの雑音指数(真値)をそれぞれの実効雑音温度に置き換えると、次のようになります。

雑音指数の測定方法
Yファクター法
Yファクタ法は、オン・オフが可能な雑音源を使用します。これは同じポート・インピーダンス3と同じ測定帯域幅で実施される2つの電力測定に基づいています。雑音源には特定の量の過剰な雑音があります。これは過剰雑音比またはENRとして指定されます。ENRは、雑音源からの雑音とシステム熱雑音またはkTBとの比率で、しばしばdBで表されます。
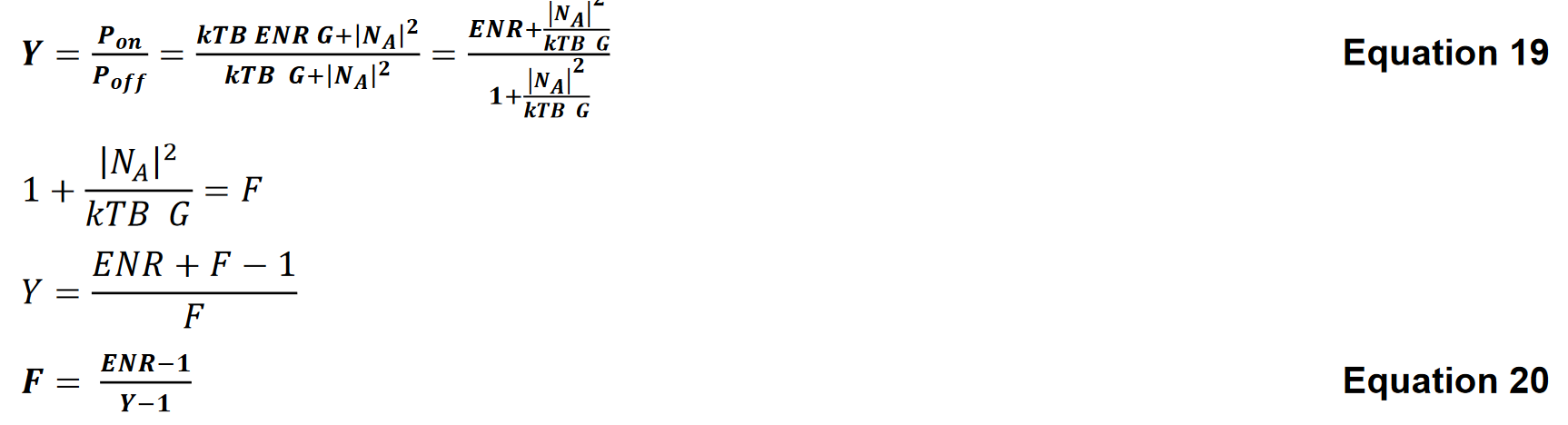
Yファクター法を使用した雑音指数(dB)の測定は、切り替え可能な雑音源と4つの電力測定を使用します。最初の2回の測定は、測定に使用される受信機の雑音の挙動を特徴づけるために使用されます。P1は雑音源がOFF状態のときに測定受信機によって測定される電力です。P2は雑音源がON状態のときに測定受信機によって測定される電力です。試験対象のデバイス(DUT)は、次の2回の電力測定のために雑音源と受信機の間に挿入されます。P3とP4は、それぞれ雑音源をOFFとONにした状態でDUT出力で行われる電力測定です。
そして、測定を行うには3つのステップがあります。最初のステップは、しばしば校正ステップと呼ばれ、電力測定に使用されるRF受信機の雑音指数(dB)を測定することです。2番目のステップは、カスケードされた受信機とDUTに対する雑音指数(dB)の測定を行うことです。次のステップは、2つの測定を分離することです。
受信機の雑音指数(dB)を次のようにしましょう。

試験対象デバイス(DUT)と受信機のカスケードの雑音指数(dB)は以下のようになります。

DUTの電力ゲインは比を取ることで測定されます。
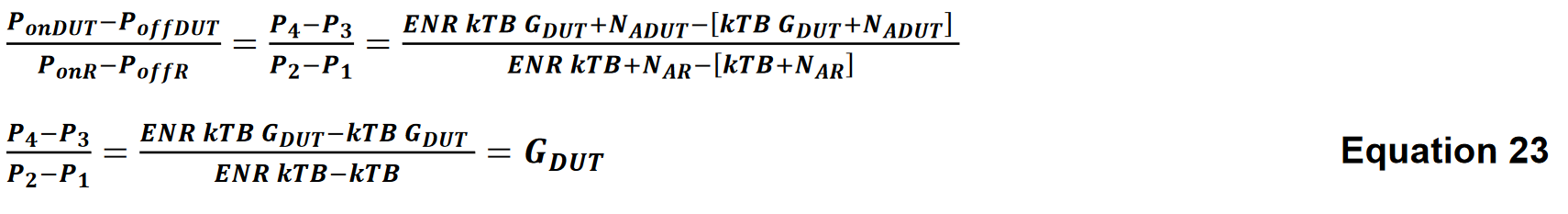
カスケードされた雑音指数(dB)の方程式から、次の式が得られます。
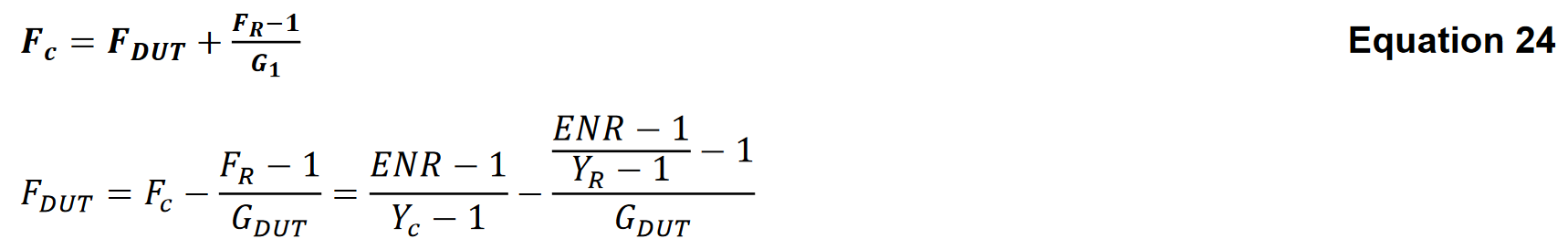
Yファクターに対する電力比を代入すると、以下が得られます。
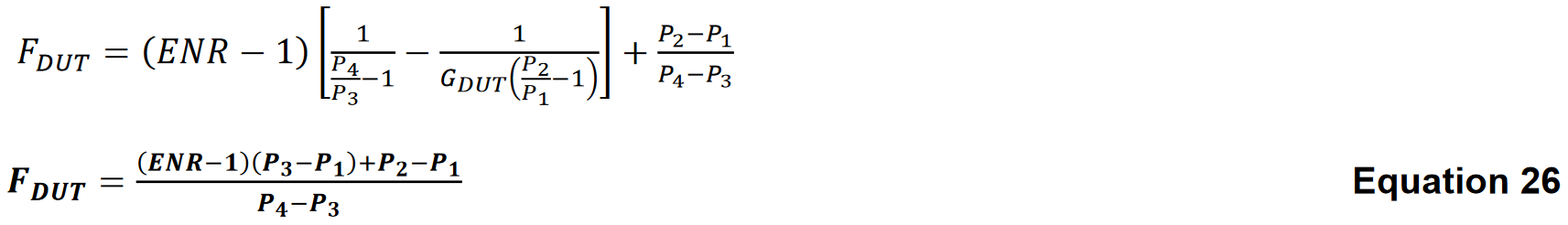

方程式26は、Yファクター法の4つの電力測定を用いて試験中のデバイスの雑音指数(dB)を表します。一連の電力測定に依存するこの方法は、低レベル測定受信機に理想的に適しています。これは現代のスペクトラム・アナライザにおいて、コスト効果の高い雑音指数(dB)測定方法として実装されています。
コールド・ソースまたはネットワーク・アナライザ法
コールド・ソース法は本質的に、参照温度(コールド)である入力を持つデバイスの出力における雑音電力を測定します。これはデバイスのゲインに関する非常に正確な知識に依存しています。ネットワーク・アナライザは非常に正確にゲインを測定することができるため、この方法に理想的です。Yファクター法と同様に、コールド・ソース法には測定受信機の雑音指数(dB)を決定するための校正ステップが必要です。これは校正された雑音源と、方程式21に記述されているものと同様の方法を用いて行われます。
試験中のデバイスのゲインは、通常のネットワーク・アナライザの方法論を用いて周波数の関数として測定されます。その後、コールド・ソースを試験中のデバイスに接続して周波数の関数として電力測定が行われます。試験中のデバイスによって加えられる雑音を NA(ω) 、受信機によって加えられる雑音を NR(ω) とした場合、測定される電力は次のとおりです。
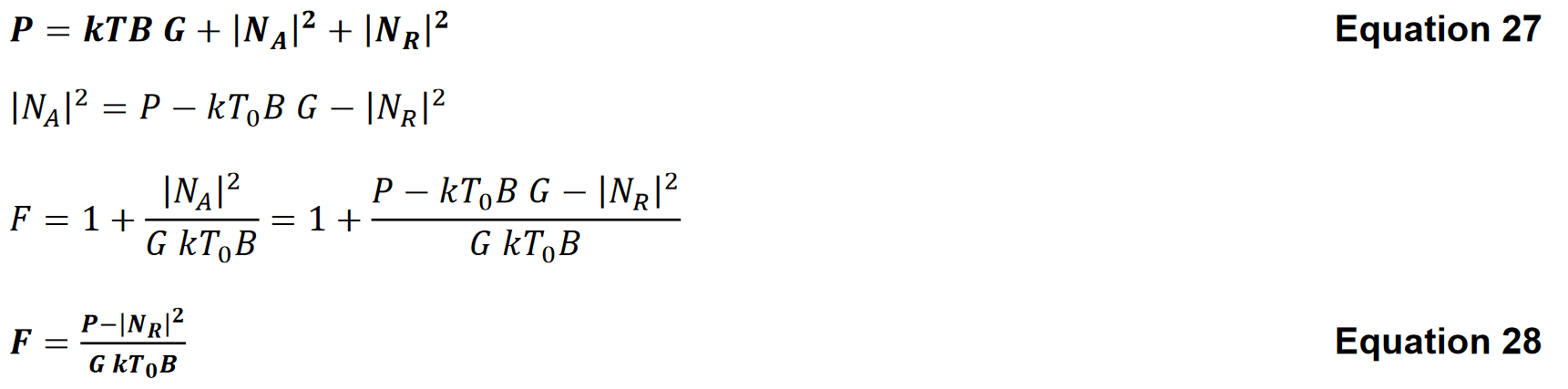
一部のネットワーク・アナライザ4は、受信機に低雑音プリアンプ、校正された雑音源、および測定を行うソフトウェアを含む雑音指数(dB)測定オプションを提供しています。ネットワーク・アナライザが正確な伝送と反射の測定を行う能力は、雑音指数(dB)とSパラメーターを含むデバイスの完全な特性評価を可能にし、ネットワーク・アナライザの測定をソフトウェアベースのシステムモデルに組み込むのに理想的です。
シグナル・ジェネレータ(トゥワイス・パワー)法
高い雑音指数(dB)を持つ測定デバイスは、人気のあるYファクター法にとって問題となります。雑音指数(dB)がソースの過剰雑音比(ENR)に近づくにつれて、Yファクターは単位に近づきます。これはYファクター測定の精度に影響します。トゥワイス・パワー法では、信号発生器と正確に既知の雑音帯域幅(BW)を持つ測定受信機(例えばスペクトラム・アナライザ)を使用します。試験中のデバイスへの入力は、概ね参照温度(通常は290K)の負荷で終端されます。次に、信号発生器が試験中のデバイスに接続され、測定される電力が正確に3dBまたは入力終端時の電力の2倍になるまで接続されます。この時点で正弦波の電力は雑音電力と完全に同じであり、雑音指数(真値)を計算することができます。受信機の帯域幅の知識は重要ですが、デバイスのゲインの知識は必要ありません。カスケードされたDUTと受信機の雑音指数(真値)は、次から計算することができます。

DUTの雑音指数(真値)は、方程式24のカスケード雑音指数(dB)の式を用いて分離することができます。
直接雑音測定法
高い雑音指数(dB)を持つデバイスは、ゲインが分かっていれば、スペクトラム・アナライザや正確に既知の帯域幅を持つ他の受信機を直接使用して測定することができます。試験中のデバイスへの入力は、参照温度(290K)に近いソースで終端されます。その出力における雑音電力が測定され、雑音指数(真値)は次から計算することができます。

受信機の帯域幅とデバイスのゲインの知識が必要です。カスケードされたDUTと受信機の雑音指数(真値)は、方程式24にあるカスケード雑音指数(dB)の式から計算することができます。
周波数変換器の雑音指数測定
スーパーヘテロダイン受信機は、今日使用されているほとんどのRF通信システムの核として存在しています。固定中間周波数(IF)で重要なフィルタリングと増幅機能を実行することで高いゲインと周波数選択性を提供する能力により、AMラジオから深宇宙プローブを追跡する受信機まで、感度の高い受信機にとって選択されるアーキテクチャとなっています。
スーパーヘテロダイン・ラジオ受信機の核は周波数変換(ミキシング)で、時にはキャリア周囲のスペクトラムに含まれる情報をIFに転送するために複数のステージで行われます。したがって、周波数変換器の雑音性能は受信機設計の重要な側面です。
受信機や周波数変換器の雑音指数(dB)、雑音指数(真値)または雑音温度を測定する方法は、上記で説明した単一周波数で動作する要素に対する方法論と似ていますが、入力の周波数帯が出力の周波数帯と同じではないという例外があります。また、ミキサーのデュアルサイドバンド性質や、サンプラーやその他の調波ミキシングデバイスにおける複数の変換を考慮に入れる必要があります。
画像除去機能を持つ周波数変換器

RF受信機で使用される典型的な周波数変換器は、ミキサーの前に画像除去フィルタを組み込んでいます。画像除去フィルタは正弦波の乗算がデュアルサイドバンドの性質を持つために必要です。
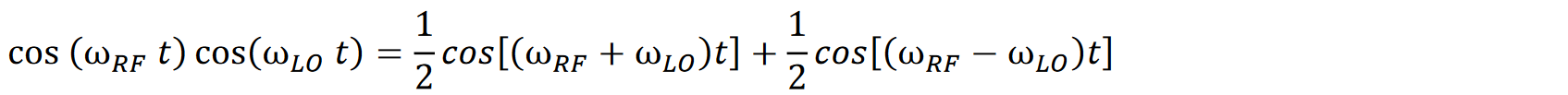
IFバンドパスフィルタによって上記の和項は除外され、IFフィルタ内に信号が現れる2つの可能性が残されます。

上記の方程式には2つの可能な解があります。

画像除去フィルタは、上側帯域または下側帯域のいずれかのみを通過させるように設計されており、図4に示されているように両方は通過させません。
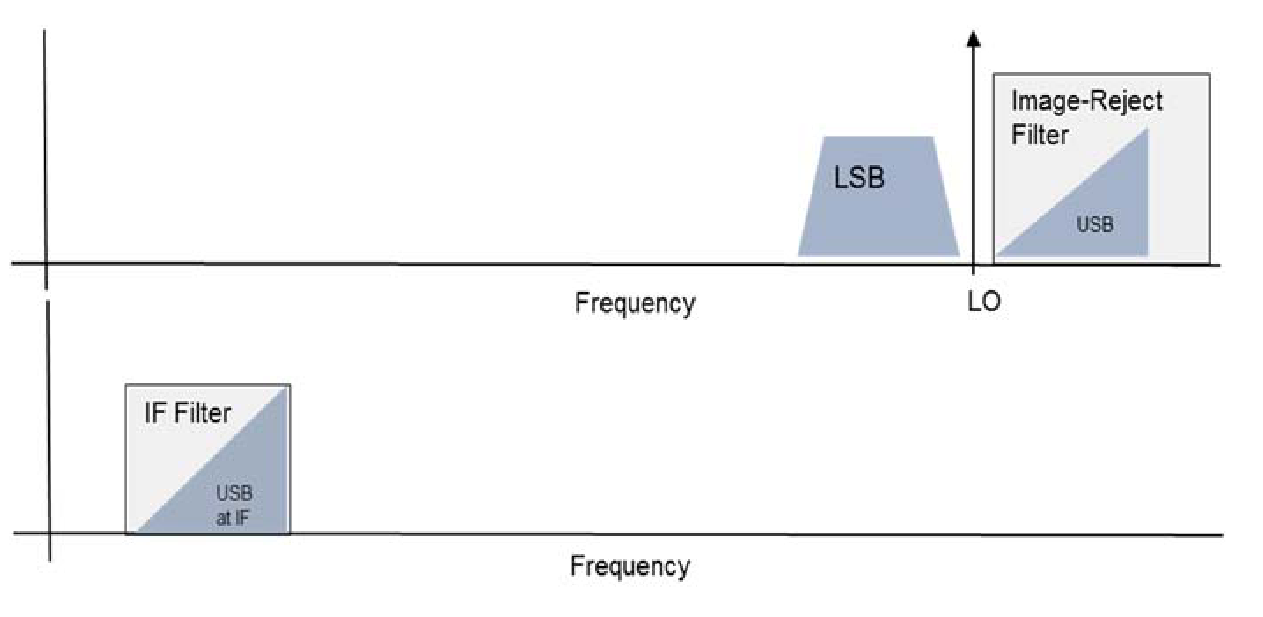
ノイズは全ての周波数にわたる周波数成分を持つブロードバンド・ランダム・プロセスとして表現できます。熱雑音は全ての抵抗性デバイスで生成されます。ショットノイズは離散的な電子の流れる粒状の電流の性質によって生成されます。図3に示されたシステムの各ステージにはノイズ・ジェネレータがあります。画像除去フィルタの前に生成されたフィルター・パスバンドの外側にあるノイズ成分はフィルタによって取り除かれます。フィルタの後に生成された両サイドバンドのノイズ成分はミキサーによって変換されます。受動フィルタは主にリアクティブであるため、熱雑音を示しません。したがって、ミキシング・ステージの回路要素によって追加される全てのノイズはフィルタリング後の要素から来ると仮定することができます。そのため、拒否されたサイドバンドの信号は存在しないにもかかわらず、IFには両サイドバンドのノイズが存在します。
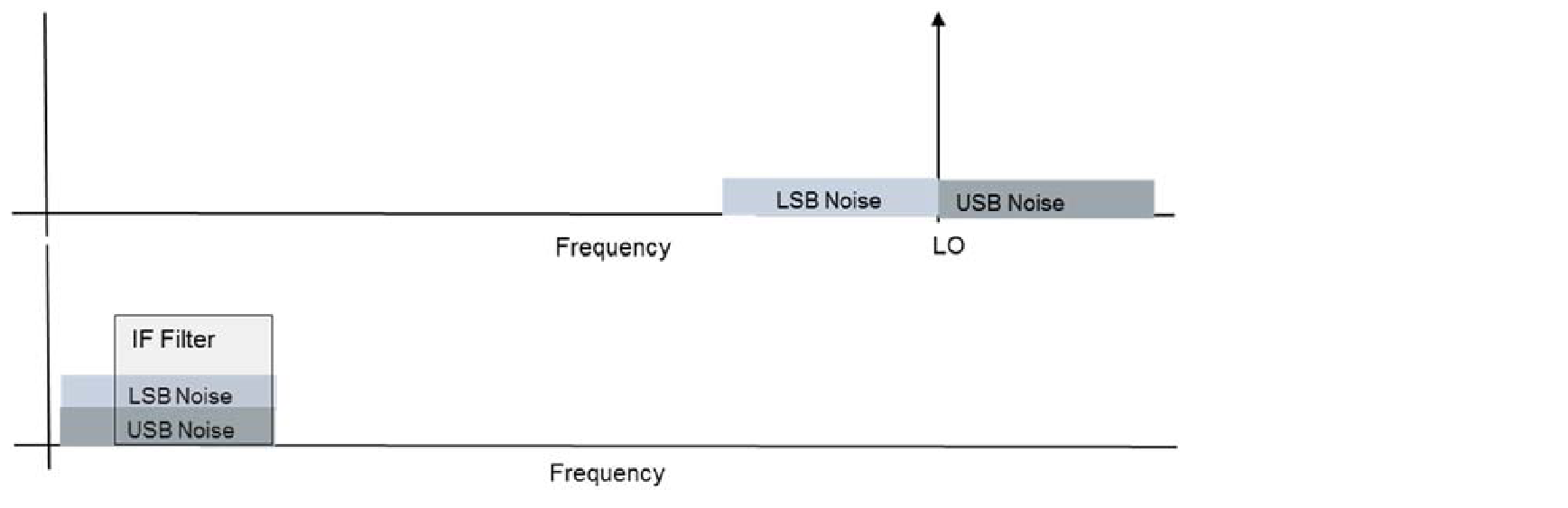
拒否されたサイドバンドからの追加ノイズは、システムによって追加された他のノイズと区別がつかず、通常、受信機の雑音指数(dB)測定に含まれます。ただし、特別な注意を要するケースもあります。
画像除去フィルタを含んだ測定
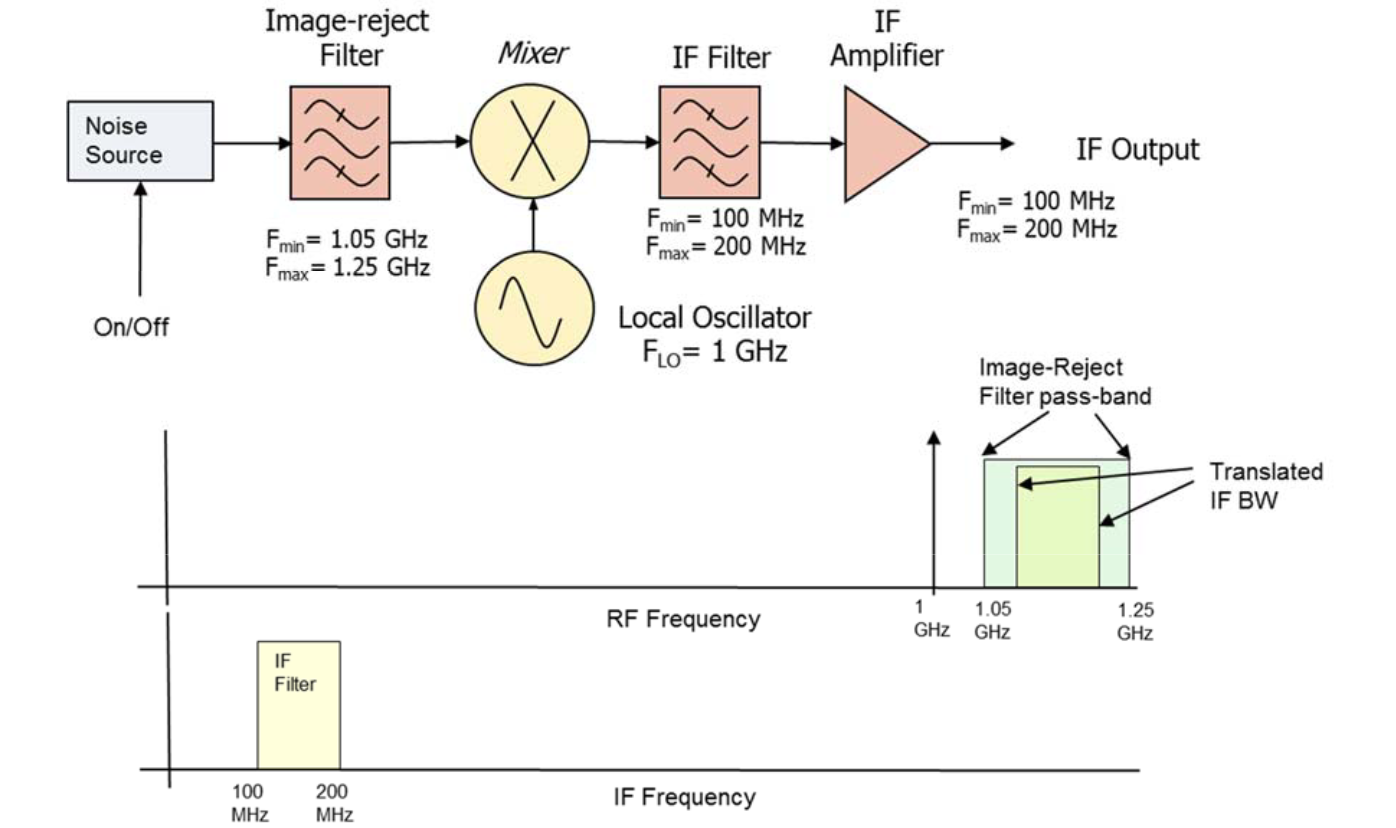
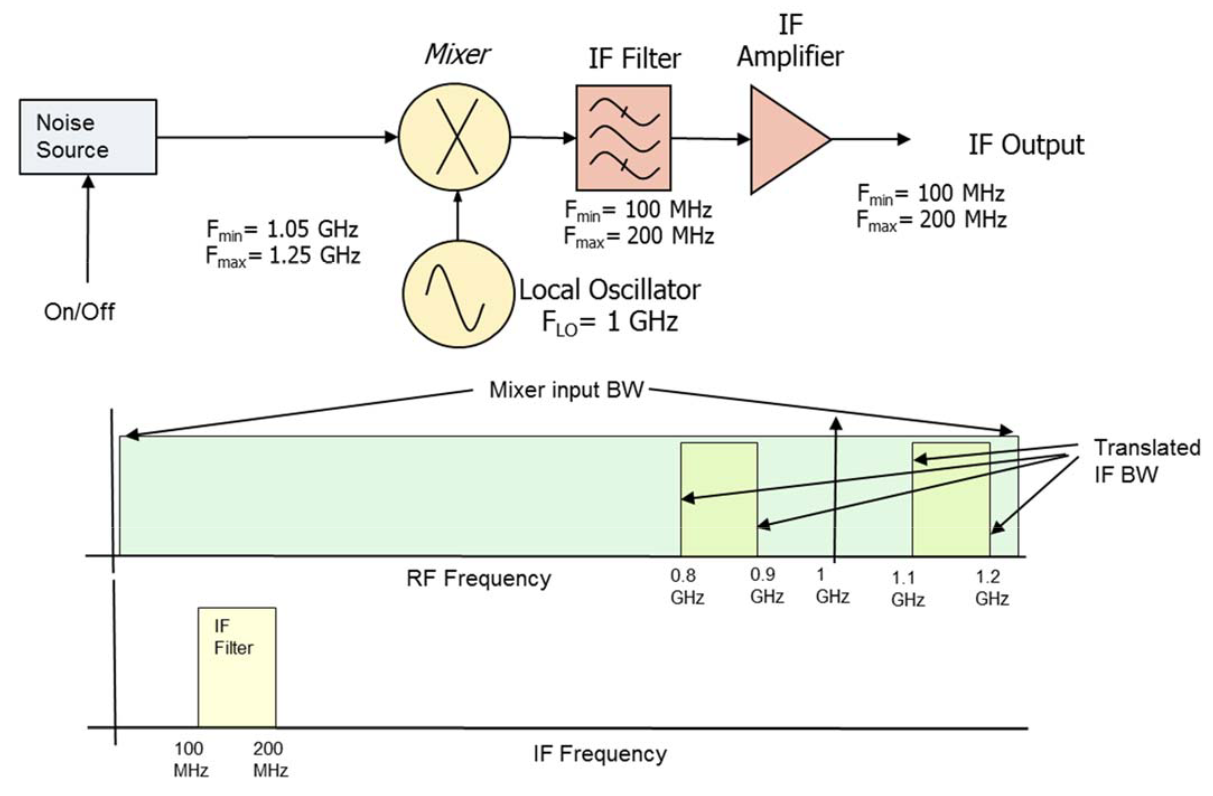
図6に示された周波数変換器システムで行われた雑音指数(dB)測定を考えます。ミキサーの前の画像除去フィルタは、望ましいサイドバンド(1.05 GHzから1.25 GHz)に入るノイズ源からの余分なノイズのみをミキサーに入れ、両サイドバンドの熱雑音がミキサーに入ることを許可します。そのようなシステムでの測定は、周波数変換器の効果を考慮する必要があることを除いて、単純です。
雑音指数(dB)測定は、方程式20から方程式23に詳述されているように、2部分で行われます。最初の部分では、測定受信機のYファクターを測定します。これはミキサーとIFフィルタの後に存在する周波数帯域で行われます。周波数変換器は、組み合わせたDUTと測定受信機のYファクター測定を、ミキサーの前に存在する周波数帯で行うための周波数変換を提供します。ノイズ電力測定を実行するスペクトラム・アナライザは、そのスパン内で100MHzから200MHzのIfをカバーするように調整する必要があります。雑音指数(dB)対周波数プロットのX軸は、1.1GHzから1.2GHzをカバーする同等のRF周波数を示す必要があります。
周波数変換器の雑音指数(dB)測定は、異なるバンドを含めるために方程式20から方程式24を変更することで調査することができます。もしミキサーの前に存在するバンドの周波数をω1とし、ミキサーの後に存在するバンドの周波数をω2とするならば、ミキサー後のバンドで行われる受信機の雑音指数(真値)は以下の通りです。

DUTと受信機のカスケードの雑音指数(dB)は、ミキサー入力バンドで測定されます。

DUTの変換ゲインは、電力比として表現され、比を取ることで測定されます。

方程式27の下付き文字1-2は、問題のゲインが周波数変換ゲイン、またはω1での電力とω2での電力の比率であることを示しています。
カスケードされた雑音指数(dB)の方程式から、次の式が得られます。

重要な点として、方程式35で使用される過剰雑音比(ENR)には2つの異なる値があることに注意する必要があります。IF(ミキサー出力周波数)でのノイズ源のENRは、受信機単体を測定する際に使用されます。ミキサー入力周波数でのノイズ源のENRは、周波数変換器が測定に含まれる場合に使用されます。
画像除去フィルタを含まない測定
モジュラー・システムでは、画像除去フィルタをミキサーやIFフィルタとは別のモジュールに配置することがよくあります。意図された画像除去フィルタから分離された周波数変換器での雑音指数(dB)測定を行うことは、しばしば有益です。そのようなシステムでの測定には、図7に示されるように、上側と下側の両方のサイドバンドからのノイズ成分が含まれます。測定は、画像除去フィルタを含む運用環境と、それを含まないテスト環境の違いを考慮して調整する必要があります。
図7は、画像除去フィルタが含まれていない測定の例を示しています。ノイズ源は上側と下側のサイドバンドの両方でノイズを寄与し、それらはIFで同じ帯域に変換されます。
受信機を測定するためのYファクター測定方程式は方程式18から変わりません。両側帯域変換器のYファクター測定方程式は、両側帯域からの寄与を考慮して修正される必要があります。もしENRUω1 とENRLω1 がそれぞれ上側と下側のサイドバンドでの過剰雑音比であり、GUω1-2 とGLω1-2が電力比として表現された上側と下側のサイドバンド変換ゲイン(または損失)であり、|NA(ω2)2|がミキサー後の周波数に関して周波数変換器ステージによって加えられるノイズである場合、
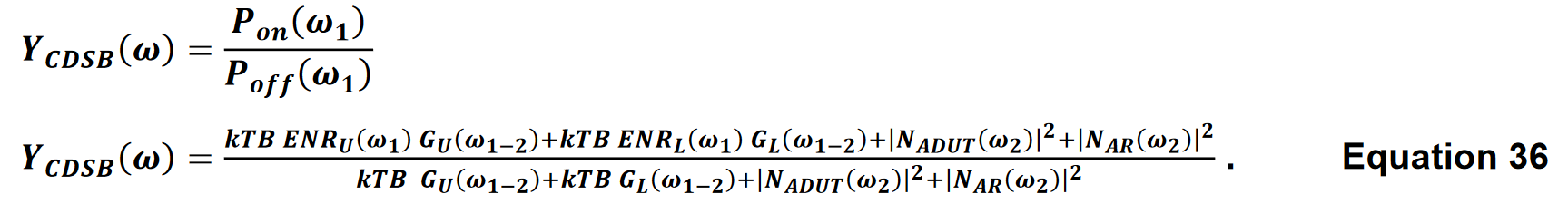
周波数変換器の両側帯域変換ゲインは、比を取ることで測定することができます。
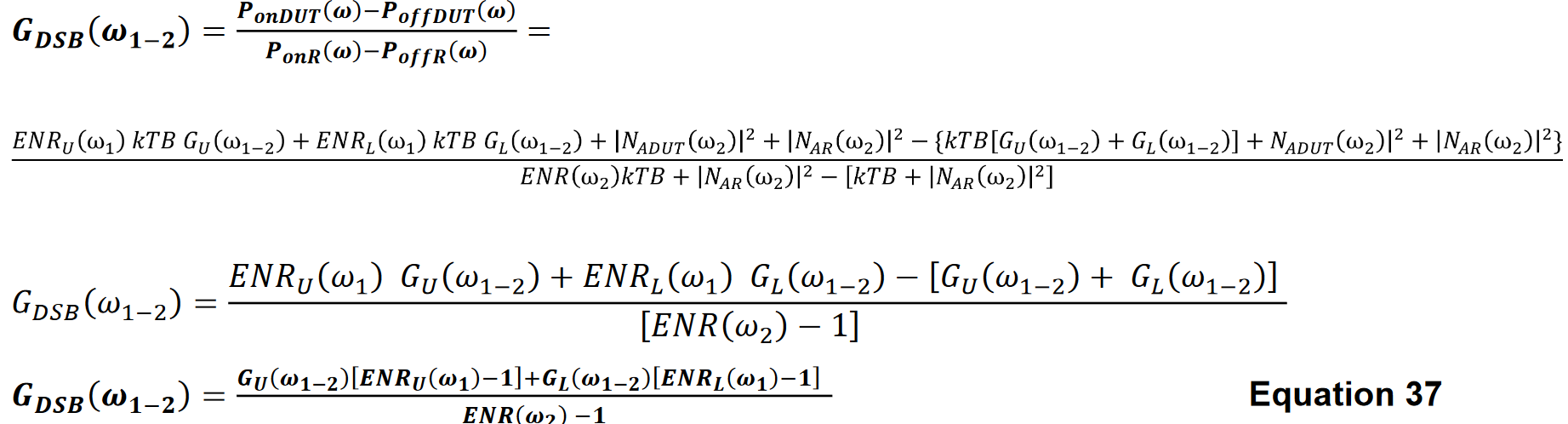
方程式37の有用な特別なケースは、ノイズ源のENRとミキサー変換ゲインが周波数に対して一定である場合です。

その場合、方程式37は次のように単純化されます。

このケースでは、両側帯域のゲインは単側帯域のケースの2倍になります。
受信機のYファクターは、ミキサーの後に存在する周波数帯で測定されます。

カスケードされた周波数変換器と受信機のYファクターは測定可能です。この測定分析には上側帯域と下側帯域の両方が含まれる必要があります。上側帯域のENRとゲインを示すために添え字Uを、下側帯域を示すために添え字Lを使います。

方程式31より、
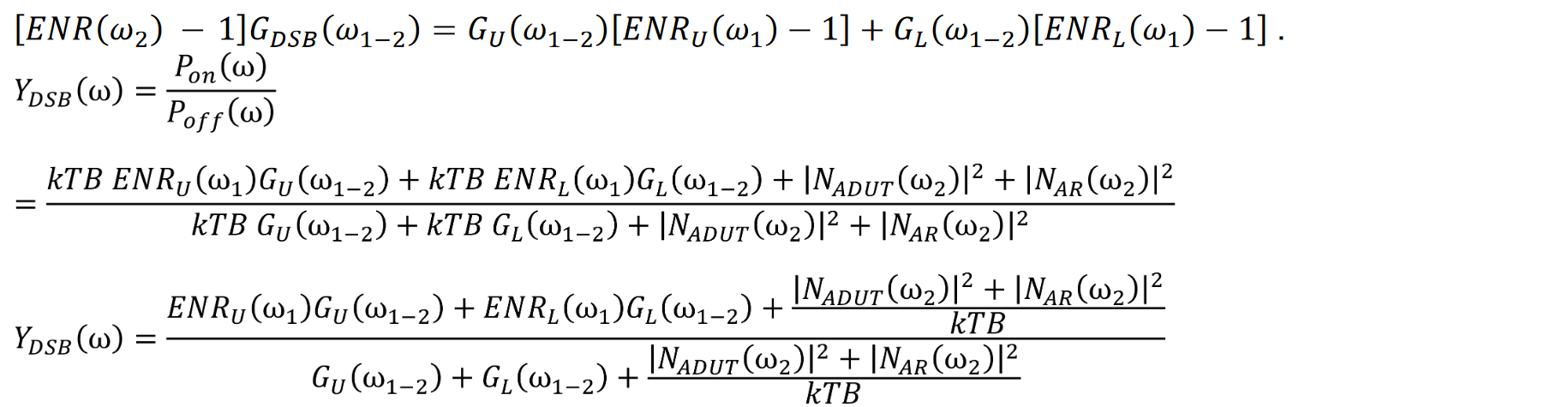
一般的に、雑音指数(dB)は方程式19を使用して計算できます。便宜上ここに再掲します。

両側帯域ミキサーを測定する場合、ENRには3つの可能な値を考慮する必要があります。ENR_L(ω1)とENR_U(ω1)はミキサー入力での下側帯域と上側帯域の過剰雑音比を指します。ENR(ω2)は混合後に存在する帯域の過剰雑音比を指します。ENR_DSB(ω1)を効果的な両側帯域ENRとして定義しましょう。

以下のようにします。

カスケード雑音指数(真値)の方程式から
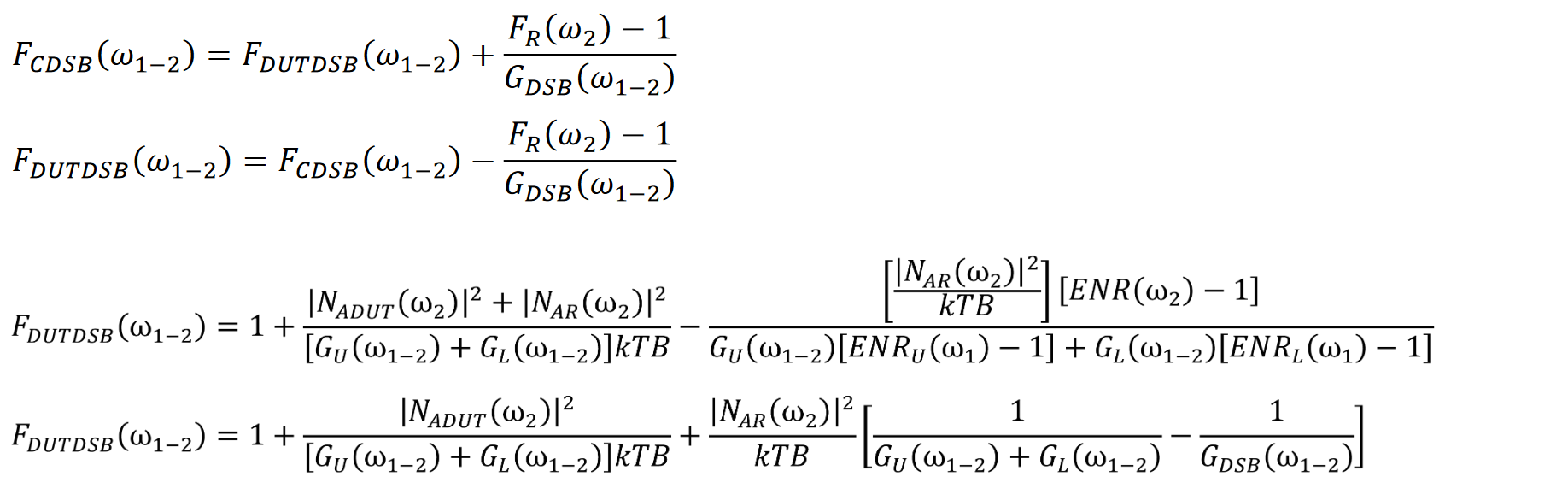
上側帯域と下側帯域で変換ゲインが一定の場合

画像除去フィルタが測定に含まれる場合の雑音指数(真値)については、次の点に注意する必要があります。

方程式42を下側帯域に拡張することができます。上側帯域と下側帯域の変換ゲインが等しく、ENRがフラットな場合には、
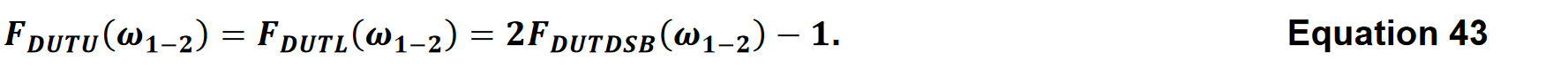
ランダム・ノイズの性質
熱雑音
宇宙のすべては動いています。見かけ上静止している物体でさえ、その分子はランダムな振動をしています。このランダムな振動は熱として人間の感覚に感じられます。実際、温度はこれらのランダムな振動の平均的な運動エネルギーを測るものです。絶縁体、導体、半導体の分子、電荷担体(電子やホール)および電子デバイスが構築されるすべての物理的構造についても同じことが言えます。熱雑音からの電力は次のように与えられます。

かっこの中身は平均として表される統計的な量を示しています。方程式44のPn = kTB における変数は次の通りです。
Pn = ワットで表される雑音電力
T = ケルビンで表される絶対温度
B = ヘルツで表される帯域幅
k = 1.3806488 x 10−23 J/k = ボルツマン定数
電子部品から発生する熱雑音は、電圧と電流の変動として現れます。電圧と電流の統計的分布は、限られた帯域幅内で観測されるとほぼガウス分布を示します。
熱雑音のパワースペクトル密度
理想的な抵抗器における熱雑音は、RFおよびマイクロ波エンジニアが使用するほとんどの周波数でおおよそ白色です。このフラットな周波数分布からの逸脱は、電磁波の量子的性質が支配的になる非常に高い周波数で存在します。雑音電力は次から得ることができます。5

方程式45には、プランク定数hを使用した光子エネルギーhfが含まれています。多くの場合、RFおよびマイクロ波エンジニアによって使用される動作周波数は、hf / kT ≪ 1であり、方程式46は熱雑音のためのフラットなパワースペクトル密度を示すおなじみの方程式Pn(f) = kTBに単純化されます。例外は非常に低い雑音温度と非常に高い周波数で発生します。
図8には、雑音のパワースペクトル密度に色をつける量子効果が示されています。熱雑音は量子効果が支配的になる100GHz以上までフラットなパワースペクトル密度を持つと考えることができます。

ショット・ノイズ
エンジニアは通常、電流を連続した量と考えます。実際には、それぞれ固定された電荷を持つ離散的な電子から構成されています。電流は量子化されています。連続的な流れではなく、電流は回路内で源から負荷まで移動する個々の電子の影響から構成されています。電子は時間を通じて一様な分布で到着します。この到着時間の変動の効果はショット・ノイズまたは粒子ノイズと呼ばれます。付録2ではショット・ノイズのパワースペクトル密度についての方程式が導出されています。雑音電力は電流に比例します。効果的な雑音電流はRMS値または標準偏差によって与えられるガウス分布に近似されます。

i/fノイズ
パワースペクトラム密度がおおよそi/fに比例して変化するランダムな変動は、ナイル川の氾濫パターンから人間の脳ニューロンの発火に至るまで、多くのプロセスで観察されています。また、いくつかのノイズ現象は非常に低い周波数で白色ノイズから逸脱を示します。このいわゆるi/fノイズまたはピンク・ノイズは、周波数に反比例する曲線に近いパワースペクトラム密度を持っています。それは低周波数で支配的になることがありますが、数Hzから数kHzの周波数範囲でフラットな熱ノイズ以下に低下し、その低下はデバイスによって異なります。6
ノイズ・パワースペクトル密度グラフ
以下のグラフは、1Hzから始まり、温度が290Kで1014Hzまで拡張される電子部品からの雑音のパワースペクトル密度を示しています。低周波数では1/f効果が現れ、そのパワースペクトル密度が熱雑音のそれを下回るまで支配的です。非常に高い周波数には量子効果が含まれます。パワースペクトル密度は、電子デバイスが操作するほとんどの周波数範囲でフラットとみなすことができます。

電子部品における雑音
すべての物質は熱エネルギーの結果として分子振動を経験します。実際に温度は動いている分子の平均的な運動エネルギーを測る尺度です。電子デバイスも例外ではありません。すべての電子デバイスは、分子の振動により、あるレベルで雑音を発生させます。
抵抗器
抵抗器は、その内部分子のランダムな変動によって熱雑音を発生させます。抵抗器の雑音寄与を、その等価雑音電圧または等価雑音電流の観点から考慮することがしばしば有用です。これらの値は、キットの知識や粒子の熱エネルギー(熱ノイズフロア)から導出することができます。抵抗器における熱雑音によって引き起こされる等価雑音電圧の導出は、付録1に示されており、以下のように与えられます。抵抗器における熱雑音によって引き起こされる等価雑音電圧の導出は、付録1に示されており、以下のように与えられます。

等価熱雑音電流は以下の式で与えられます。

抵抗器の雑音電力はフラットなパワースペクトル密度を持ち、温度と抵抗器の値のみに依存します。
コンデンサ(キャパシタ)
理想的なコンデンサは、すべてのリアクティブ要素と同様に、熱雑音を示しません。しかし、コンデンサは不完全な導体と誘電体で作られているため、関連する抵抗があります。コンデンサからの雑音電圧は、抵抗器とコンデンサの並列組み合わせを含む回路の雑音電圧から導出することができます。抵抗器を無限大にすると、付録1に示されているように、コンデンサ単体から放出される熱雑音電力が得られます。

有効な並列抵抗器を無限大にすると興味深い結果が得られます。全周波数にわたって積分された全雑音電力は、温度と静電容量値のみに依存します。

インダクタ
理想的なインダクタは、すべてのリアクティブ要素と同様に、熱雑音を示しません。しかし、実際の誘導性コンポーネントには、巻線と磁気コアに損失があります。これらの損失は、雑音を発生させることが示される等価直列抵抗器としてモデル化することができます。付録1には、インダクタの雑音の導出が示されています。それはインダクタの実効直列抵抗にのみ依存しており、以下のように与えられます。

アクティブ・デバイス
能動部品には多くの雑音の要因があります。それぞれの抵抗素子は熱雑音を発生させます。バイアス電流はショット・ノイズに寄与します。すべての回路要素の内部リアクタンスは雑音のパワースペクトル分布を形成します。回路要素内のすべての雑音源を図10に示されるオペアンプの等価雑音電圧と電流の観点からモデル化することはしばしば有益です。
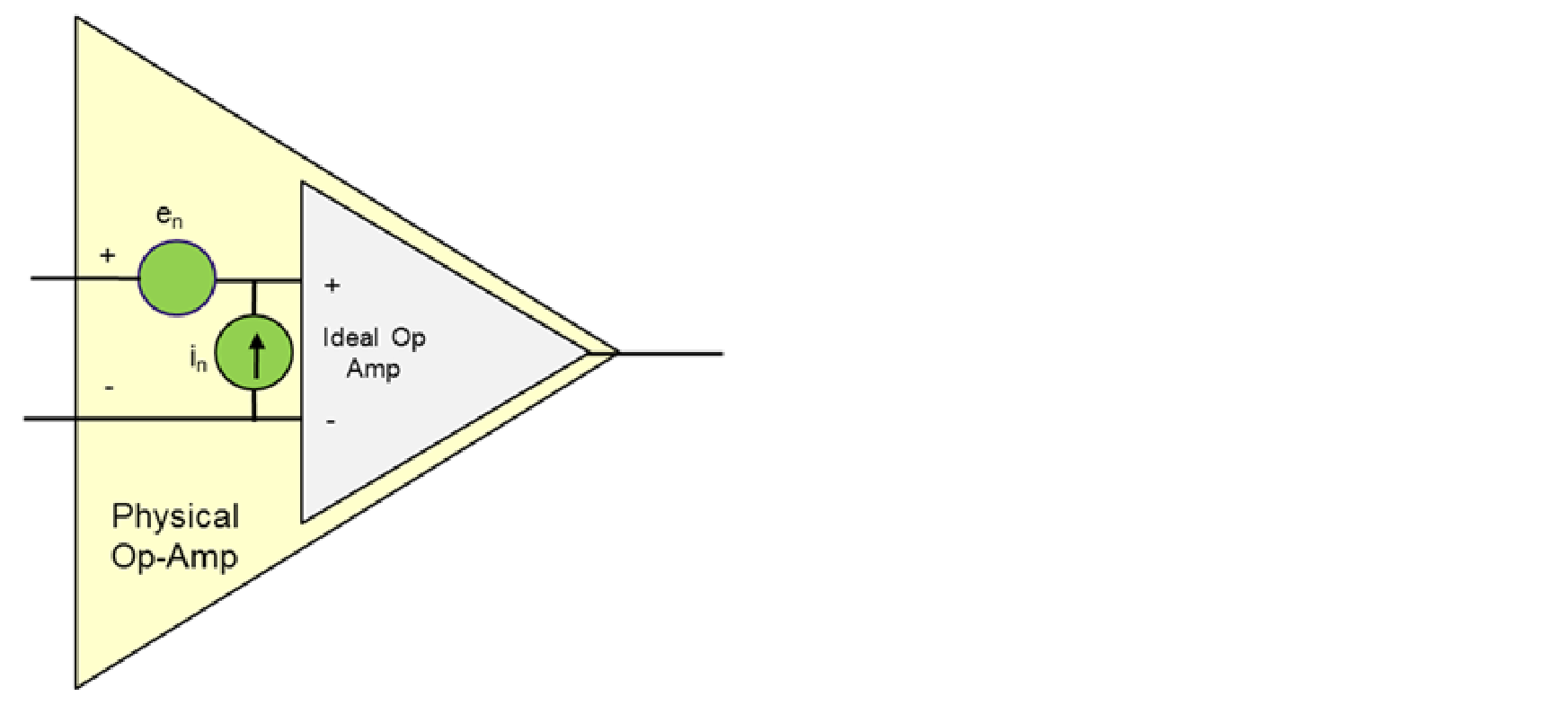
実際のオペアンプは理想的な無雑音オペアンプとしてモデル化され、入力に雑音電圧と雑音電流が加えられます。雑音の寄与は、アンプ出力の等価雑音源でモデル化することもできます。雑音電圧と雑音電流はオペアンプ内のすべての回路要素の総合的な寄与を表しています。抵抗素子は熱による寄与があります。バイアス電流はショット・ノイズを発生させます。リアクティブ素子は雑音のパワースペクトル分布を形作ることができます。トランジスタ、RFアンプ、およびすべてのアクティブ・コンポーネントはこの方法でモデル化することができます。等価雑音源の実際の値は、アンプの内部回路を慎重にモデリングするか、測定によって確定することができます。
まとめ|雑音指数とノイズ測定
電子システムには必ずノイズが存在します。ノイズを適切に測定、モデリングし、そのシステムへの影響を考慮することは、非常に小さな信号から情報を抽出する必要があるRFおよびマイクロ波受信機において重要な懸念事項です。回路要素によって加えられたノイズは、受信される信号を隠したり曖昧にしたりすることがあり、信号の障害を引き起こします。
回路要素のノイズ寄与を雑音指数(真値)または雑音指数(dB)の形で測定することは、RFおよびマイクロ波エンジニアにとって重要な仕事です。このホワイトペーパーとその付録は、Yファクター・メソッドとそれに関連する測定不確かさに焦点を当てたノイズ測定方法の概要を提示しています。
1 このホワイトペーパーでは、すべての追加されたノイズをアンプの出力に割り当てます。追加されたノイズがDUTの入力でモデル化される他の導出も存在します。
2 Friis, H.T., Noise Figures of Radio Receivers, Proc. Of the IRE, July, 1944, pp 419-422
3 「ON」と「OFF」の状態でポート・インピーダンスが変化するノイズ源は、雑音指数測定に追加の誤差をもたらします。
4 Agilent Application Note: High Accuracy Noise Figure Measurements Using the PNA‐X Series Network Analyzer.
5 Kerr.A.R and Nanda, J. P. 42
6 Johnson, J. B. (1925)
ノイズ測定に最適な製品
ノイズ測定に最適なテクトロニクス製品をご紹介します。
RSA306B型USBスペクトラム/シグナル・アナライザは、小型・軽量でありながら、優れた性能を備えています。お客様が2倍のサイズで2倍の価格のスペクトラム・アナライザに求めてきた機能を搭載しています。さまざまな測定にご活用いただけます。

RSA500シリーズ・リアルタイム・スペクトラム・アナライザ
高度なスペクトラム解析機能を備えた、小型・軽量で堅牢なRSA500シリーズ・スペクトラム・アナライザを使用することで、高精度のリアルタイム測定が行えます。最高40GHzの周波数帯域に対応し、VLFバンドからKuバンドまでの9kHz~18.0GHzの信号をすばやく捕捉できます。

RSA600シリーズ・リアルタイム・スペクトラム・アナライザ
高確度のRSA603A型/RSA607A型USBスペクトラム・アナライザは、無線デバイスの統合やEMI、IoTプロジェクトに役立つ豊富な機能を備えており、デバイスやコンポーネントの視覚化/特性評価に最適です。
クラス最大のディスプレイ、優れたレベル信号測定確度、業界をリードするプローブ性能を備えた3シリーズMDOは、ベンチ・オシロスコープの新しい基準を打ち立てます。IoT用のベースバンド設計をテストする場合、または単純なEMI傍受を行う場合でも、3シリーズは独自のハードウェア・スペクトラム・アナライザを内蔵しているため、優れたRFテスト性能と保証されたRF仕様を備えています。
SignalVu-PC RFスペクトラム・アナライザ・ソフトウェア
SignalVu-PCには、スペクトラム解析、ベクトル信号解析、復調などのための以下のような包括的なマルチドメイン・ツール・セットが用意されています。
- テクトロニクスの RSAシグナル・アナライザによるリアルタイム解析
- テクトロニクスのオシロスコープによるワイドバンド解析
- テクトロニクスのすべてのスペクトラム・アナライザとオシロスコープで取込んだ波形のオフライン解析
ノイズ測定の関連資料
ノイズ測定に関する、閲覧数の多い人気資料をご紹介します。
製品についてご不明な点ございましたら、お気軽にお問い合わせください。


