最近の数多くの AC 電源アプリケーションに伴う複雑な電流/電圧波形のため、さまざまな測定上の課題が発生しています。このような問題に対処する場合、基本的な測定、使用される用語、それらの関係について理解することが重要になります。このアプリケーションノートではパワー測定の基本的な考え方やパワー測定において重要な、以下の用語の明確に定義します
- RMS(Root Mean Square value、実効値)
- 電力
- 有効電力(W)と皮相電力(VA)
- 力率
- クレスト・ファクタ
- 高調波歪み
RMS(Root Mean Square value、実効値)
実効値は、AC の電圧と電流両方の値を規定する、最も一般的で便利な値です。AC 波形の実効値はその波形から得られるパワーのレベルを示すものであり、AC 信号の最も重要な属性となります。
実効値の計算は、AC の電流波形と、それによって生じる発熱効果によってうまく説明できます(図 1a 参照)。
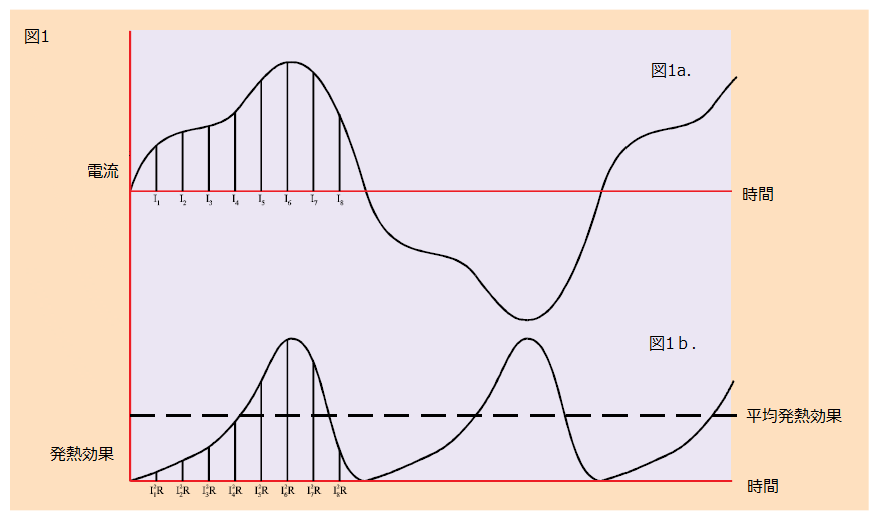
この電流が抵抗に流れたとすると、任意の時間における発熱効果は次のように計算できます。
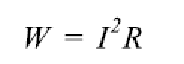
電流波形を均等に分割すると、時間による発熱効果の変動は図 1b のようになります。
発熱効果の平均値(電力)は、次のように求められます。
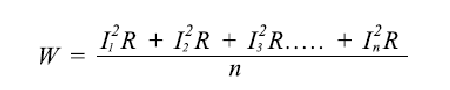
上記で示した平均発熱効果を発生させる電流と等価の値を求めるには、次のようになり、
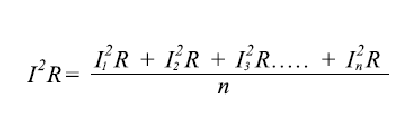
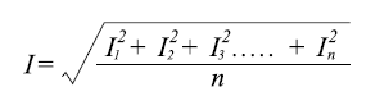
=電流の二乗平均平方根
=電流の実効値
この値は、抵抗負荷に発熱効果(電力)を発生させる DC 電流と等価であるため、AC 波形の実効値と呼ばれることがあります。 正弦波の場合は、このような計算をしなくてもシンプルに次式で表せます。
実効値=ピーク値/√2
すなわち、実効値=0.707×ピーク値
平均値
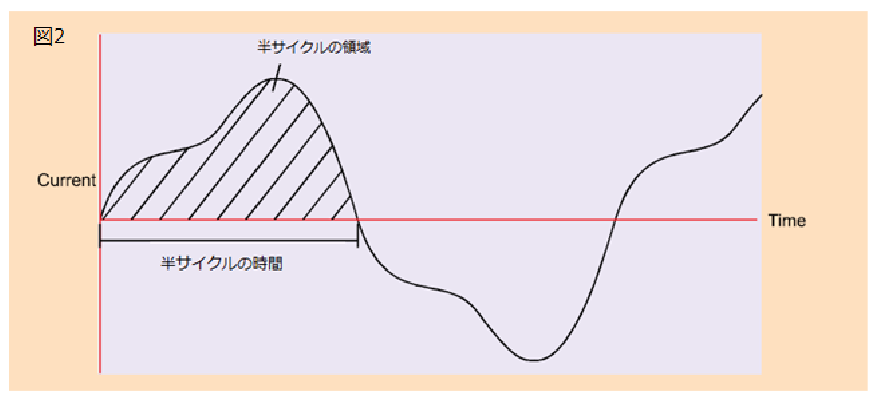
図 2 のような波形の平均値は、次のように求められます。
平均値=(半サイクルで囲まれた領域)/(半サイクルの時間長)
平均値は波形の半サイクルに対して意味を持ち、対称性のある波形の完全な 1 サイクルにおける平均値はゼロになります。シンプルなマルチメータでは、AC 波形を全波整流した波形の平均値を計算します
しかし、このようなマルチメータは実効値で校正されており、正弦波の実効値と平均値の以下のような関係性(波形率)を利用しています。
実効値=1.11×平均値
しかし、純粋な正弦波以外では、このようなマルチメータの読み値は有効ではありません。
有効電力(W)と皮相電力(VA)
100Vrms の正弦波電圧が 100Ωの抵抗負荷に接続されると、電圧と電流は図 3a のように表され、「同相」であると言います。電源から負荷に流れる、任意の時点における電力はその時点における電圧と電流の積となり、図 3b のようになります。
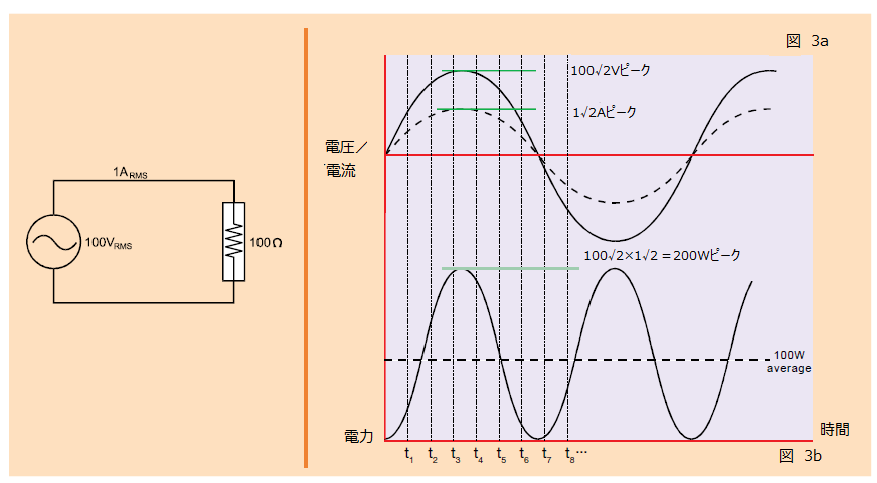
この結果、負荷に流れる電力は 0~200W で変動し(電源の 2 倍の周波数)、平均電力は 100W となります。これが 100Ωの抵抗における 100Vrms で得られる値になります。
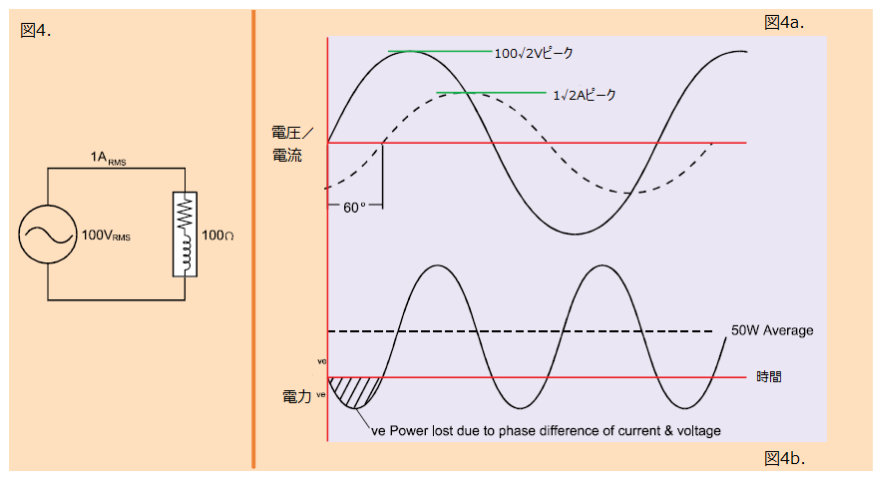
しかし、負荷が 100Ωのインピーダンスとリアクタンス性(例えば、抵抗と同様にインダクタンス、キャパシタンスの負荷)を持っている場合、電流は 1Arms ですが電圧と同相にはなりません。誘導性負荷の場合の例を図 4a に示します。電流は 60°遅れています。
電力は電源の 2 倍の周波数で変動していますが、電源から負荷へ流れる電力は半サイクルの一部しか負荷に流れていません。残りの部分は負荷から電源に向かって流れています。したがって、負荷に流れる平均値は抵抗負荷のみの場合と比べると小さくなり、図 4b に示すように利用可能な電力のうち、50W のみが誘導性を含む負荷に供給されます。
上記の 2 つの例における実効値電圧は 100Vrms であり、実効値電流は 1Arms となります。この 2 つの値の積は負荷に供給される皮相電力であり、次のように VA で表わされます。
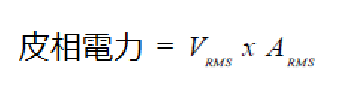
供給される有効電力は、負荷によって異なります。電圧と電流の実効値のみがわかっていても、有効電力の値を求めることはできません。瞬時電圧と瞬時電流の積が計算でき、その結果の平均値が表示できる真の AC パワー・メータを利用しない限り、有効電力あるいは熱損失や効率などは評価できません。
力率
DC システムとは違い、伝送される AC 電力は電圧と電流の値を掛け合わせて求められるほど簡単ではありません。さらに、力率という要素も考慮しなければなりません。先に説明した誘導負荷を含む例(有効電力と皮相電力)では、利用可能な電力は皮相電力のちょうど半分でしたので、力率は 0.5 になります。力率は、次のように求められます。
力率=有効電力/皮相電力
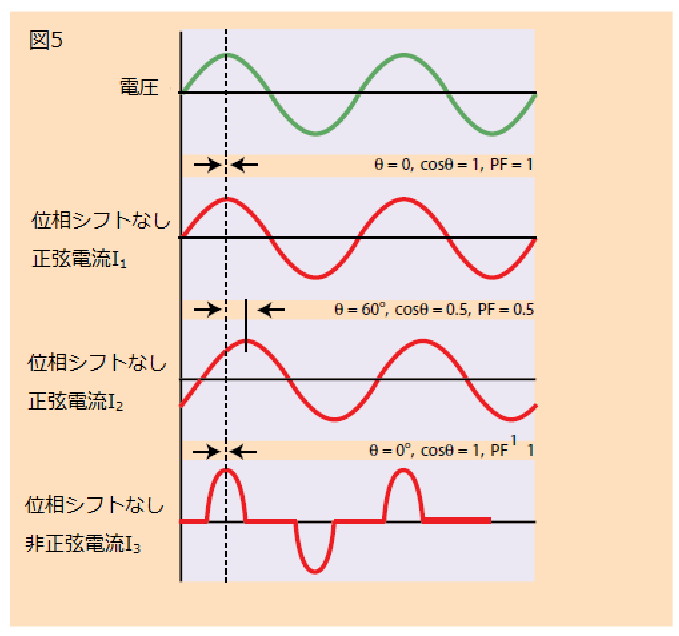
正弦波の電圧および電流波形の場合、力率は電圧と電流波形の位相角(θ)のコサインになります。例えば、先に説明した例の誘導負荷では、電流は電圧から 60°遅れます。したがって、
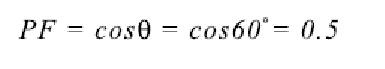
力率が cosθと表現される理由がここにあります。しかし、これは電圧と電流が正弦波(図 5 の I1、I2)の場合にのみ当てはまることであり、その他の場合(I3)では力率は cosθにはなりません。cosθの値を表示する力率計を使用する場合、電圧、電流が純粋な正弦波でない場合、cosθの読み値は正しくないことを思い出す必要があります。真の力率計は、上記で説明したように、電力の有効成分と皮相成分の比を計算します。
クレスト・ファクタ
先に説明したように、正弦波では以下の式が成り立ちます。
ピーク値=実効値×√2
ピーク値と実効値の関係はクレスト・ファクタで表され、次式で示されます。
クレスト・ファクタ=ピーク値/実効値
正弦波の場合は次のようになります。
クレスト・ファクタ=√2/1.41
AC 電源に接続される最近の機器には、非正弦波の電流が流れるものが数多くあります。このような電源には、ランプの調光器や蛍光灯も含まれます。
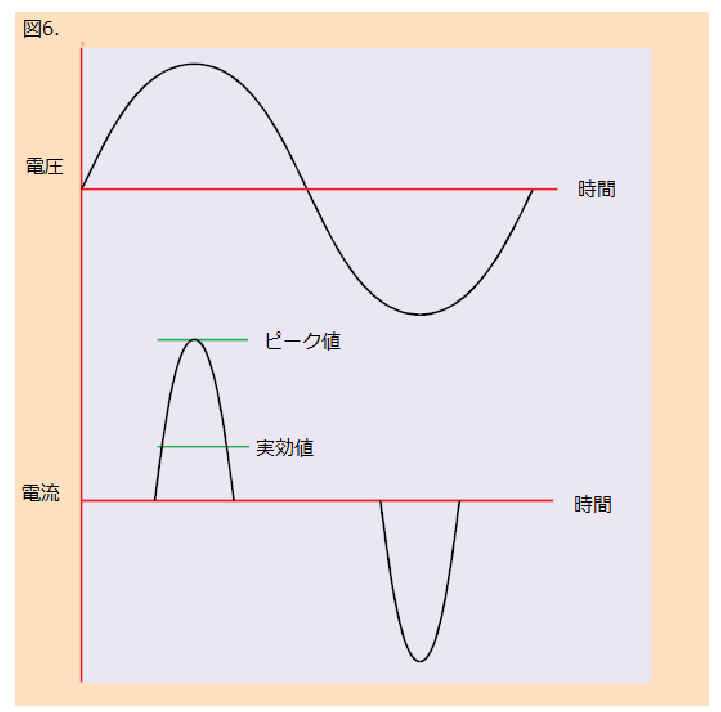
一般的なスイッチング電源は、図 6 に示すように AC 電源から電流を取り込みます。電流波形のクレスト・ファクタは1.414 よりも大きくなることは明らかであり、ほとんどのスイッチング電源、モータ速度コントローラの電流クレスト・ファクタは 3 以上になっています。機器には大きなピーク電流と歪んだ波形が入力されるため、大きな電流クレスト・ファクタは AC 電源に大きなストレスを加えることになります。これは、スタンバイ・インバータなどのように、限られたソース・インピーダンスから負荷に電力を供給する場合に顕著となります。したがって、AC 機器の電流の実効値だけでなく、クレスト・ファクタを知ることが重要です。
高調波歪み
負荷によって電流波形に歪みが生ずる場合、クレスト・ファクタに加え、波形形状の歪みレベルを定量化することも重要です。DPOPWR のような専用の解析ソフトウェアがない場合、通常のオシロスコープで歪みは観測できますが、歪みのレベルまでは測定できません。
フーリエ解析によると、非正弦波の電流波形は、電源周波数の基本波成分と、電源周波数の整数倍の周波数成分を持った一連の高調波で構成されます。例えば、100Hz の方形波は図 7 に示すような成分で構成されます。方形波は、純粋な正弦波に比べると非常に歪んでいます。しかし、スイッチング電源、調光器、速度制御している洗濯機のモータなどの電流波形は、より大きな歪み成分を含んでいることがあります。図 8 は、一般的なスイッチング電源の電流波形と、その電流による高調波成分を示しています。
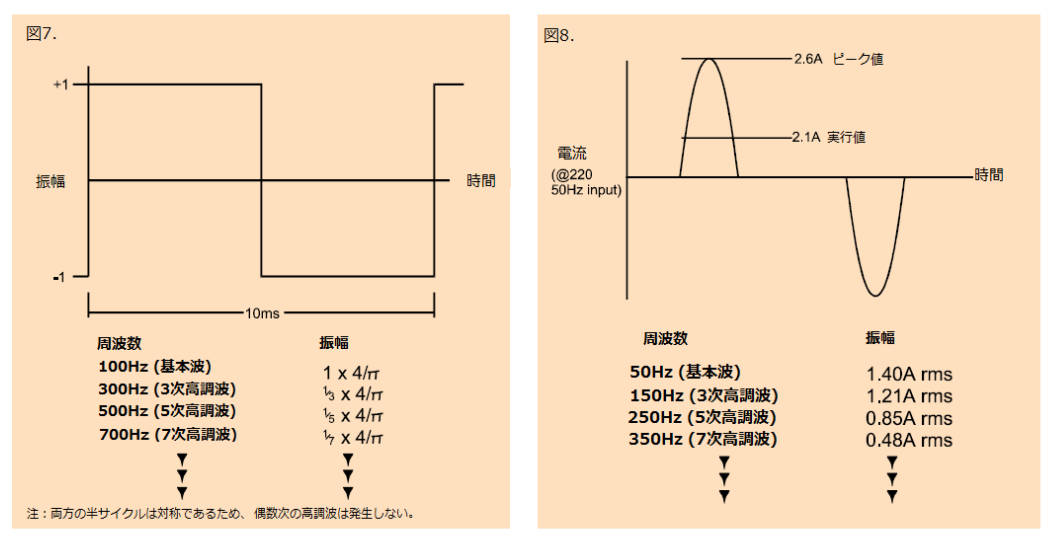
有効な電力を生成できるのは、電流の基本波成分のみです。その他の高調波成分は電源内部を流れるだけでなく、配線ケーブル、変圧器、電源に関連したスイッチング素子にも流れるため、これらすべてで更なる損失が発生します。
機器が発生させる高調波のレベルを制限する必要性が認識され始めています。負荷の種類に応じて順守すべき高調波電流の許容レベルが国/地域ごとに規定されています。このような規制は広まっており、EN61000-3 などの国際的な規格もあります。したがって、機器の設計エンジニアも設計した製品が高調波を発生させていないか、また、どの程度の高調波が発生しているのかを認識する必要があります。
AC パラメータの測定
機器の製造メーカ、AC 電源の製造メーカにとって、ここで説明した AC パラメータが重要であることを解説してきました。しかし、このようなアプリケーションで利用される機器は使いづらかったり、必要な機能が提供できなかったり、特に、解析される信号がノイズを含んでいたり、歪んでいるような場合は要求される高確度を実現できなかったりすることがあります。
Tektronix は、汎用的な電力測定から複雑な最新の電力解析までの、さまざまなアプリケーションに適したソリューションに対応した電力測定機器を開発、製造しています。

