Chapter 1: Introduction
The MDO4000 Series from Tektronix represents a new paradigm in instrumentation; the Mixed Domain Oscilloscope, or MDO. These are the first instruments that are designed specifically to make synchronized or time-correlated measurements between digital, analog, and RF signals simultaneously in both the time and frequency domains.
This document introduces this new instrument category by presenting:
- A discussion of the trends that drive the need for the MDO4000C
- A summary of the capabilities found in the MDO4000C
- A primer on the technology used in the MDO4000C
Trend: Wireless is Everywhere
In recent years, there has been an explosion in the use of wireless technology for data transfer. In almost every industry, wireless links are replacing or extending traditional wired communications. Examples include:
- Wireless wall switches and dimmers for lighting
- Wireless control / display panels for utilitarian products such as water softeners
- Wireless data connections for home stereo
- Wireless tire pressure monitoring sensors
- Wireless connections between portable video game consoles
The proliferation of wireless technology is comprised of both licensed and unlicensed band technologies. Predominantly, a licensed band technology is used by a broadcaster or service provider (TV, radio, cell phone), while unlicensed technology operates over much shorter ranges in “free bands” (Bluetooth, Wireless LAN, garage door openers, remote keyless entry).
Modern wireless systems use sophisticated modulation schemes. These modulation schemes are generally implemented by using digital signal processing, DSP, and can be expressed in Cartesian complex form of I (In-Phase) and Q (Quadrature) data which, in turn, is used to modulate the transmitted RF signal.
Almost by definition, then, modern wireless technologies span both time and frequency domains. In addition, the signals exist in three domains: digital, analog, and RF.
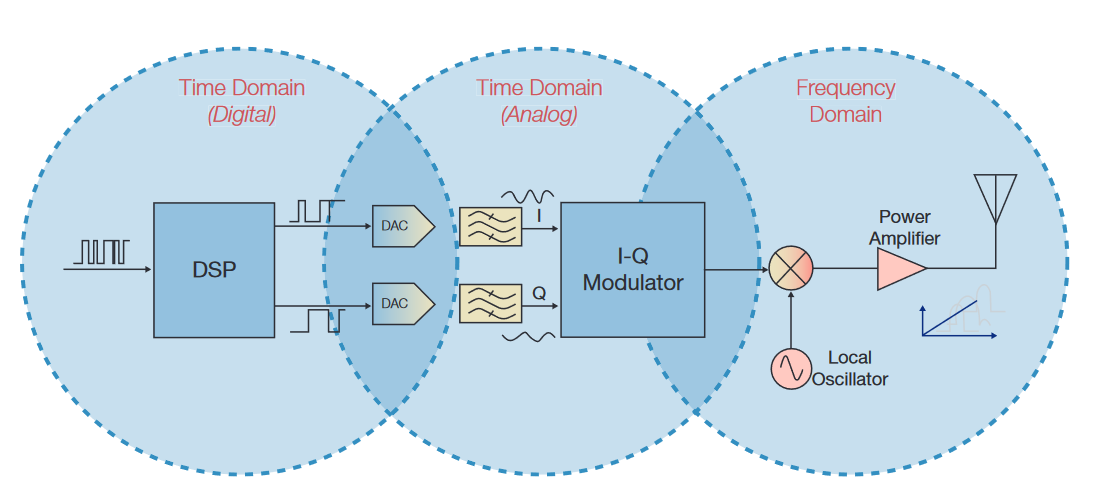
Designers are struggling to make the measurements necessary to design, troubleshoot, and verify systems that cross these three measurement domains. Prior to the introduction of the Tektronix Mixed Domain Oscilloscopes, no single instrument had been optimized for these types of measurements.
What is needed is a measurement tool that is specifically designed for making measurements in all three domains.
Trend: Today’s Embedded Designer’s Responsibilities are Expanding
This trend toward wireless everywhere is causing a profound change in the responsibilities of embedded designers as they struggle to incorporate unfamiliar RF technology into their designs.
Embedded designers frequently find themselves needing to solve problems without the proper equipment needed to perform the tasks. Examples include:
- Designing and troubleshooting a simple RF link, using ASK or FSK techniques
- Determining if a Bluetooth radio IC is transmitting when it is supposed to
- Troubleshooting the programming of an IEEE 802.11 chipset during operation
- Detecting and synchronizing multiple wireless technologies on the same device in the same frequency bands to avoid self-jamming
- Tracing the handshake between a radio transmitter and receiver as communication is established
The tool of choice for the embedded designer, the oscilloscope, is optimized for making time-domain measurements only. An MSO (Mixed Signal Oscilloscope) can measure both analog and digital signals, but it remains difficult to effectively measure RF signals with an oscilloscope at the RF carrier. It is also quite difficult to adequately correlate events in the time and frequency domains – something critical for finding system-level problems.
While spectrum analyzers are available for making measurements in the frequency domain, these are not the tool of choice for most embedded designers. Using spectrum analyzers to make time-correlated measurements with the rest of the system is virtually impossible.
What is needed is a measurement tool that extends the traditional MSO measurement strengths by allowing the user to correlate phenomena in the frequency domain with the time domain events that caused them.
Trend: Radios are Embedded Systems
Radio design has not been immune from the trend toward embedded microcontrollers that has dominated electronic design over the last 20 years. As a result, modern radios contain data busses (both serial and parallel), microcontrollers, and a significant SW component.
Radio designers frequently find themselves needing to solve problems without the proper measurement equipment. Examples include:
- Determining if a programming error is causing low transmit power
- Finding the source of intermittent crosstalk into a transmitted radio signal
- Verifying that a frequency-hopping algorithm is working correctly
The tool of choice for these designers, the swept spectrum analyzer, is optimized for measuring a single frequencydomain signal. It cannot measure time domain signals, nor can it provide any meaningful time correlation between an RF signal and the multitude of other electronic signals found in the device. The traditional swept spectrum analyzer is not suitable for investigating time-varying RF signals and woefully inadequate for debugging issues in wireless embedded systems.
A modern type of spectrum analyzer, the vector signal analyzer, has been developed to measure time-varying RF signals. In some cases, vector signal analysis software can be added to an oscilloscope to provide the analysis of timevarying RF signals; however, the oscilloscope may not be able to directly measure the RF carrier frequency or have the fidelity (dynamic range) to adequately characterize the RF signal.
While oscilloscopes are available for making multi-channel measurements in the time domain, adding vector analysis software to an oscilloscope channel may limit the basic oscilloscope functionality for coherent analysis. Having different timebase analysis lengths for digital state logic, analog, and RF signals is essential for troubleshooting embedded systems.
What is needed is a single measurement tool that integrates the modern spectrum analyzer measurement strengths (vector signal analysis) to allow the user to easily make uncompromised time-correlated analog and digital time domain measurements as well.
Trend: RF Signals are Time-Varying
Modern communications are increasingly time-varying. Radios often transmit intermittently to save power. Many modern modulation schemes, using spread spectrum techniques, encode signals across multiple frequencies.
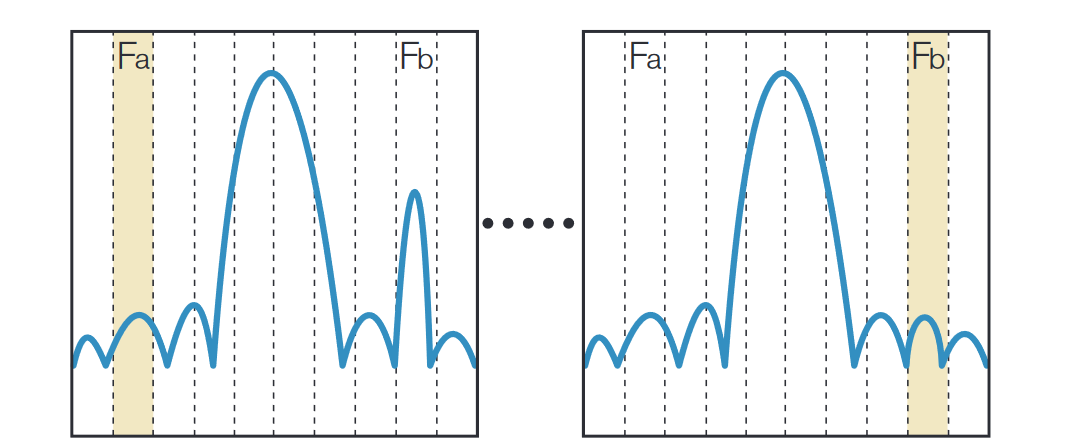
The traditional swept spectrum analyzer is a poor tool for looking at RF signals that vary with time. If a signal is not present when the analyzer is sweeping past that frequency, it will not be captured as shown in Figure 2.
A signal of interest at Fb is broadcast intermittently. As the analyzer sweeps from Fa through Fb, the signal may be missed if it does not happen to be broadcasting when the analyzer sweeps past Fb.
What is needed is a frequency-domain measurement tool with a wide capture bandwidth that can make measurements at a specific point in time, established by an event of interest in the time domain.
Trend: RF Bandwidth is Increasing / Signals are Getting Faster
Modern communications are using increasingly wide bandwidth modulation schemes, and packet communications are getting faster.
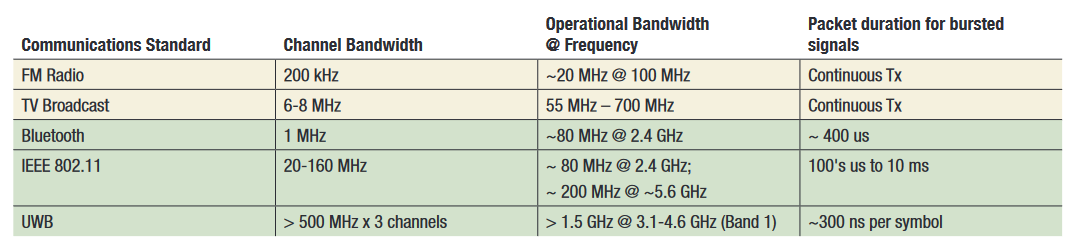
Table 1 shows a few common communications standards and their respective channel bandwidth and bandwidth of operation. Notice how channel bandwidth has increased dramatically with newer modulation schemes.
In order to effectively measure these new modern embedded wireless technologies, it is often necessary to capture the entire channel bandwidth at a single point in time.
While a traditional swept spectrum analyzer can measure continuous broadcast signals, it is not designed for measuring time-varying signals across these bandwidths. New generations of swept spectrum analyzers capture an IF bandwidth larger than the resolution bandwidth (RBW), typically 10 MHz. However, since it is swept, it cannot “see” signals outside of the current sweep frequency. The swept analyzer simply cannot capture an entire spectrum in a time-coincident manner.
Further, the time-varying nature of these modern signals is too fast for a traditional swept spectrum analyzer. Beyond the limits of the RBW, swept analyzers can take 10’s to 100’s of milliseconds for the fastest sweeps over the operational bands of interest. The transmitted signals often occur for only 10’s of microseconds or less.
More modern spectrum analyzers (vector signal analyzers) typically have a capture bandwidth of 10 MHz, making them useful for the older / simpler standards. Some spectrum analyzers are available with up to 160 MHz of bandwidth1 , making them more useful for modern standards, but this performance typically comes at a substantial price premium.
At bandwidths above this, there are really no dedicated spectral analysis tools available. Users are forced to make do with oscilloscopes or digitizers operating with specialized vector signal analysis software. Unfortunately, these timedomain solutions generally exhibit poor specifications for frequency-domain measurements, particularly in the area of spurious free dynamic range (SFDR).
What is needed is a frequency-domain measurement tool with a wide capture bandwidth and good SFDR performance
Trend: EMC is as Important as Ever
Electromagnetic Compatibility, EMC, continues to be an important element of modern electronics design. Compliance to some level of Electromagnetic Interference (EMI) testing is required for every electronic device.
It is often difficult, however, to debug and troubleshoot problems in this area. The main problem with making EMI measurements is that the regulatory frequency coverage is at least 1 GHz, and the signals being measured can be intermittent or directional.
In the traditional test setup, the electronic device is rotated in the presence of a receiving antenna so that the measurements can be made from all directions and maximized at various heights. Because of the wide frequency range, however, the rotation rate must be very slow to allow the swept analyzer to paint an accurate picture of emissions in all azimuths. Also, an emission at a fundamental frequency may be maximized at one antenna height, but its harmonic might be maximized at a different height. Understanding the emissions profile of a product under test at all test frequencies requires the ability to see all frequencies at the same time independent of antenna height.
Diagnostics become even more difficult if the source of interference is intermittent. It can be almost impossible to correlate emissions with specific events in an electronic device using traditional measurement techniques. Examples include:
- Correlating impulse emissions with specific memory access or diagnostic state of a device under test
- Characterizing emissions during the device power-up or state changes such as going in and out of low-power mode
- Understanding the relationship between emissions and higher-order harmonics
What is needed is a frequency-domain measurement tool with a wide capture bandwidth that can make measurements at a specific point in time, correlated with events of interest in the time domain.
Trend: Time to Market is More Critical than Ever
It should come as no surprise that companies everywhere are pushing to get products to market faster. Missing a market window or a design cycle can be a major setback in a competitive environment. It should be equally clear that this pressure is coming at the same time that companies are pushing toward “leaner” organizations that can do more with less.
The trends mentioned above are not well supported by current test and measurement equipment, given this increasingly high-pressure design environment:
- In order to measure signals across multiple domains, multiple pieces of measurement equipment are needed, increasing capital or rental expenses
- The methods available for making cross-domain, timecorrelated measurements, are inefficient, reducing engineering efficiency
- When only used on occasion, the learning curve to understand how to use equipment for logic analysis, time domain, and RF spectrum measurements often require an operator to re-learn each piece of separate equipment.
- The equipment needed to measure wide bandwidth, time-varying spectral signals is expensive, again increasing capital or rental expenses.
What is needed is a measurement instrument with a common user interface that integrates multiple measurement capabilities into a single cost-effective tool that can efficiently measure signals in today’s wide-bandwidth, time-correlated, cross-domain environments.
Chapter 2: The Mixed Domain Oscilloscope
The Tektronix MDO4000 Series Mixed Domain Oscilloscope (MDO) is the first tool to effectively address all of these measurement challenges for the embedded RF designer.
An MDO is an integration of a mixed signal oscilloscope and a modern spectrum analyzer. By providing unique capabilities, however, the MDO becomes truly greater than the sum of its parts. This section explores these unique capabilities and provides some insight to common applications.
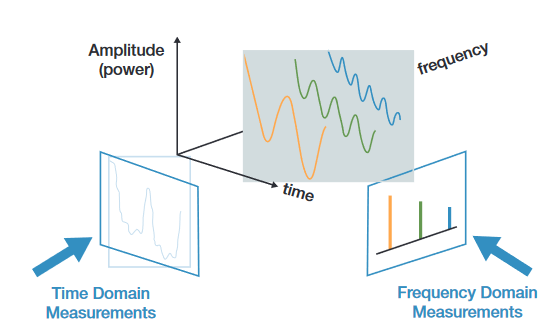
The primary value of a mixed domain oscilloscope is its ability to maketime-correlated measurements across two domains; the time domain and the frequency domain. In addition, it can make these measurements between multiple analog, digital, and RF signals.
Time-correlated means that the mixed domain oscilloscope can measure timing relationships between all of its inputs. It can, for instance, measure the time between a control signal and the beginning of a radio transmission, measure the risetime of a transmitted radio signal, or measure the time between symbols in a wireless data stream. A power supply voltage dip during a device state change can be analyzed and correlated to the impact on the RF signal. Time correlation is critical for understanding complete system operation: cause and effect.
Time-Domain signals are signals that are best viewed as amplitude vs. time. These are the signals traditionally measured with an oscilloscope. Viewing signals as amplitude vs. time helps answer questions like; “is this power supply really DC,” “is there sufficient setup time on this digital signal,” “is my RF signal on,” or “what information is currently being sent over this wired bus?” Time-domain signals are not limited to analog inputs. Seeing RF amplitude, frequency, and phase versus time can enable a study of simple analog modulations, turn-on, and settling behavior of RF signals.
Frequency-Domain signals are signals that are best viewed as amplitude vs. frequency. These are the signals traditionally measured with a spectrum analyzer. Viewing signals as amplitude vs. frequency helps answer questions like; “is this transmitted RF signal within its allocated spectrum,” “is the harmonic distortion on this signal causing problems in my device,” or “are there any signals present within this frequency band?
Analog signals are the most general of electrical signals. Many physical phenomena can be translated to analog signals with the aid of a transducer. Basically, an analog signal is a quantity (voltage, current, etc.) that varies continuously as time progresses. Analog signals represent continuously variable phenomenon, such as a power supply output voltage, or a phase lock loop control voltage.
Digital signals are dominant in modern electronics. These signals are used to encode digital information, in binary format, by switching between two distinct levels. In reality, digital signals are analog signals but it is often unnecessary (and sometimes confusing) to view them as anything more than a logic level “1” or a “0”. Digital signals are typically used for control or to encode information (in the time domain).
RF signals can be categorized as intentional and unintentional signals. Unintentional signals can be categorized as electromagnetic emissions (EMI), while intentional RF signals are dominant in modern wireless communications. These intentional signals are characterized by their encoding of information in a defined band of frequencies. This is often best analyzed in the frequency domain. RF signals are analog signals as well, but their modulation schemes, frequencies, and wireless transmission put them into a category of their own.
Traditionally, three different instruments were needed to make measurements on the signals discussed here:
- The oscilloscope, which is optimized for making timecorrelated measurements on analog signals in the time domain
- The logic analyzer, which is optimized for making timecorrelated measurements on digital signals in the time domain. Often, a mixed signal oscilloscope, MSO, is substituted for simplicity. A mixed signal oscilloscope is an oscilloscope with additional logic or digital channels that are optimized for digital signals and serial bus decode / triggering
- The modern spectrum analyzer, which is optimized for making measurements on RF signals in the frequency domain and are based on a vector signal analysis architecture
The MDO4000C mixed domain oscilloscope is the first instrument optimized for making time-correlated measurements on all three types of signals – analog, digital, and RF – across both time and frequency domains in a single instrument.
The MDO: Better than an Oscilloscope
Most oscilloscopes have the capability of calculating and displaying a Fast Fourier Transform, FFT, of the acquired time-domain signal. On the surface, this would seem to provide adequate frequency-domain analysis capabilities for many users. The typical oscilloscope, even with FFT capability, is sub-optimal for making the required measurements on RF signals.
The MDO has four major benefits, when compared against a typical oscilloscope (even with FFT capability):
- An integrated spectrum analyzer provides superior capability and fidelity for frequency-domain measurements
- An architecture that allows independent setting of acquisition parameters on the time- and frequency-domain channels
- Acquisitions across all inputs that can be sample-aligned and time-correlated across all domains
- A user interface optimized for displaying and controlling Spectrum Analysis functions

Integrated Spectrum Analyzer
The first main benefit is in acquisition capability. The MDO4000C can optionally include an integrated spectrum analyzer to the base oscilloscope. In addition to a separate dedicated input to measure RF signals, this input provides several major advantages:
- Large input frequency range
- Superior fidelity
- Low noise performance
- Integrated sample alignment
- Shared and integrated triggering capabilities with all other inputs
In order to make spectral measurements, an input capable of measuring high frequency signals is required. Many modern communications signals operate in the ISM bands at 2.4 and 5.8 GHz. Even making measurements on a relatively low frequency 900 MHz system requires an input frequency range of 4.5 GHz to examine the fifth harmonic.
While oscilloscopes are available with bandwidths that can measure these signals, they can be expensive to cover the frequency ranges required for the measurements and are not optimized for the sensitivity of RF analysis. The integrated spectrum analyzer in the MDO4000C provides the required performance for typical RF signals without requiring the other analog channels to equal that performance. Thus, adequate performance levels are achieved on both analog and RF channels while keeping the price of the instrument in line with a mainstream oscilloscope. The available models which include an integrated spectrum analyzer are shown in Table 2.
Of equal importance when making measurements on RF signals is signal fidelity.
The most important measure of fidelity in a spectrum analyzer is Spurious Free Dynamic Range, (SFDR). This multi-faceted specification indicates the ability for a spectrum analyzer to detect and measure small signals in the presence of large signals.
Input related spurs are those that are produced as a result of interactions between the user’s signal and the measuring instrument. They are difficult to “work around,” since their frequency and amplitude change with the changing input signal.
Residual spurs are those that are caused by signals generated within the measurement instrument leaking into the signal path. They are easier to identify, since they are generally static, but can be mistaken for spurs in the user’s signal.
Because of their general purpose nature, oscilloscopes typically exhibit poorer SFDR than a typical spectrum analyzer.
Low noise performance is important for measuring low level signals, and out-of-band emissions for transmitters.
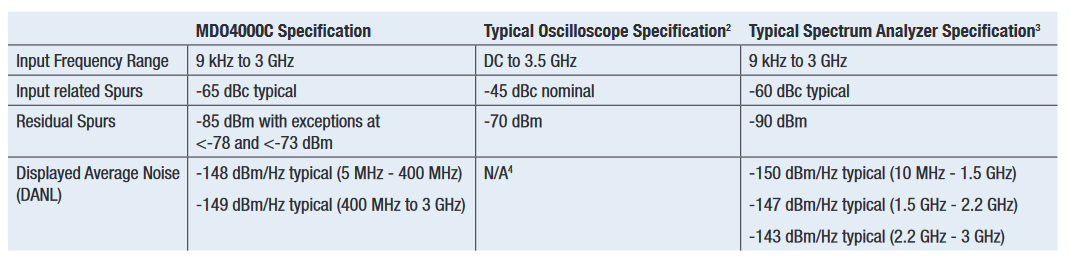
Again, the integrated spectrum analyzer in the MDO4000C mixed domain oscilloscopes addresses these concerns with superior fidelity that closes the gap between these product categories. Some key specifications are listed in Table 3.
These MDO performance improvements over an oscilloscope are made possible because the dedicated spectrum analyzer input allows the use of dedicated and optimized RF circuit elements, along with advanced signal processing techniques such as additive dither to improve linearity. These techniques cannot be used with a typical analog oscilloscope input because the use of some RF circuit elements could impact measurements down to DC, and the use of dither would be visible, as noise, in the time domain.
Independent Time- and Frequency-Domain Acquisition
The second main benefit is found in the independence of the controls and setup of the spectrum analyzer from the other oscilloscope channels. One downside of using an FFT on an oscilloscope for making frequency-domain measurements is that the settings for sample rate and record length, required for a particular frequency-domain measurement, affect the other oscilloscope channels as well. This generally means that measurements can only be made in one domain at a time. When used for frequency-domain measurements, the time-domain display is usually of little value. When used for time-domain measurements, the frequency-domain display is usually of little value. For more information on the interaction between time- and frequency-domain settings, see Acquiring the Raw RF Time Domain Data Record in Chapter 3.
Modern communications are increasingly time-varying. Radios often transmit intermittently to save power. Many modern modulation schemes, using spread spectrum techniques, encode signals across multiple frequencies.



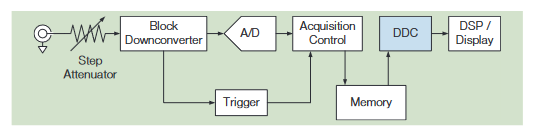
This limitation can be seen by looking at a typical 4-channel oscilloscope architecture shown in Figure 3.
By contrast, the MDO has a dedicated, independent acquisition system associated with the spectrum analyzer. This allows independent control of the acquisition parameters for optimal display when making frequency-domain measurements. In a like fashion, the time-domain acquisition parameters can still be optimized for display in that domain. These two acquisition domains are synchronized so that their data is time-correlated. This can be seen in the MDO4000C architecture shown in Figure 4.
User Interface Optimized for Frequency-Domain Measurements
The final benefit is found in the user interface. Another significant issue when using an FFT on a typical oscilloscope for making frequency-domain measurements is that the user interface is optimized for time-domain measurements. This makes it quite difficult to make typical spectrum analyzer adjustments, such as center frequency, span, and RBW. Adjusting the display typically involves manual calculations of the time-domain parameters of sample rate, record length and FFT window shape. It is also often impossible to get exactly the desired settings.
In addition, the FFT is usually displayed in the same fashion, and often in the same window, as the time-domain traces, resulting in confusing displays.
The MDO4000C eliminates these problems by providing an intuitive user interface and display that is optimized for analyzing both time and frequency domains simultaneously while maintaining time-correlation between domains at all times.
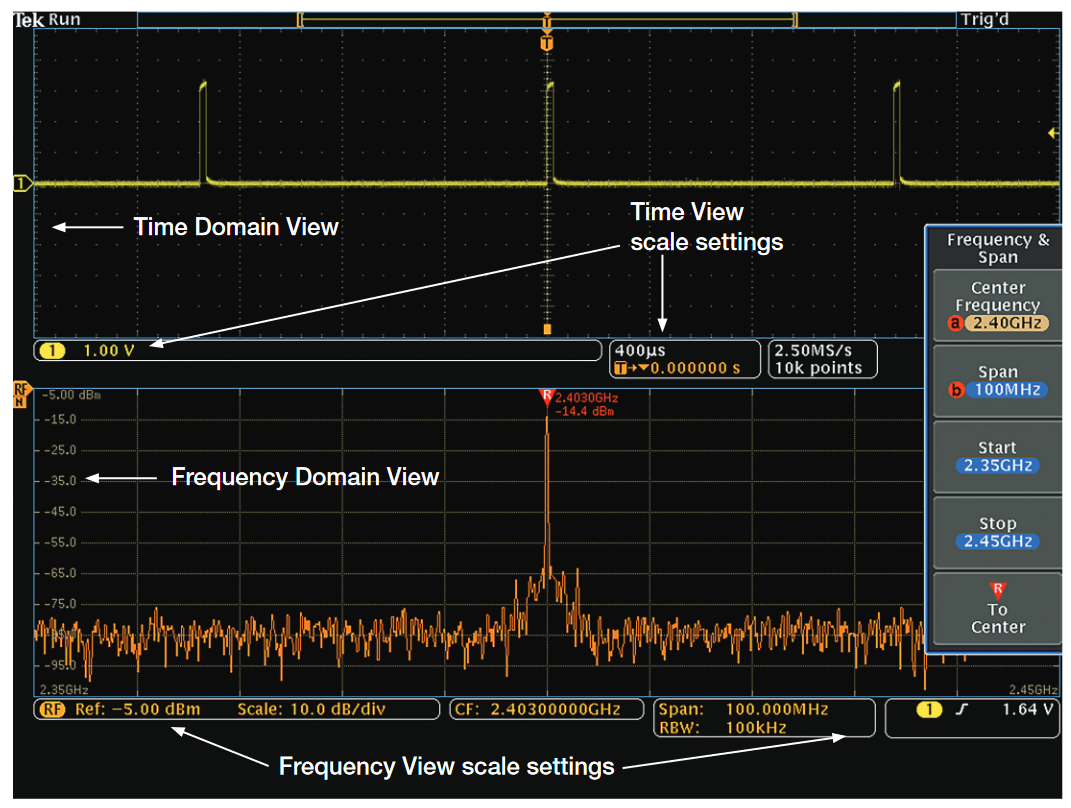
Perhaps more important, the user interface is also optimized for simultaneously viewing both time- and frequency-domain signals, providing valuable insights of interactions between these domains.
Figure 6 illustrates the dedicated nature of the user interface and display. Additional detail is provided in The MDO4000C: Powerful Combination of Capabilities later in this chapter.
Notice the following:
- Time-domain data displayed in the top display window
- Frequency-domain data displayed in the bottom display window
- Appropriate readouts for each window
- Appropriate frequency-domain menu entries
The MDO: Better than a Spectrum Analyzer
Most spectrum analyzers have the capability of displaying time-domain data, in the form of a “zero span” display. On the surface, this would seem to provide adequate timedomain analysis capabilities for many users. The reality, however, is that the typical spectrum analyzer, even with zero span capability, is sub-optimal for making time-domain measurements.
The MDO has several major benefits, when compared against a typical spectrum analyzer:
- Multiple input channels that provide system-level insight
- An integrated spectrum analyzer that provide insight with concurrent correlated frequency- and time-domain views
- Ability to see RF signals versus time without the architectural limitations of a traditional spectrum analyzer
- A time-based, wide-capture-bandwidth acquisition architecture that allows easy analysis of time-varying, wide-bandwidth and fast-occurring RF signals
Multiple Input Channels
The first main benefit is afforded by multiple input channels. The MDO4000C can be configured to include the 4 analog channels and 16 digital channels found in most MSOs to produce a product capable of measuring signals beyond the single-channel capabilities of the typical spectrum analyzer.
Modern RF signals are generated, received, and managed by complex embedded systems. Serial and parallel data buses are used to communicate between components. Power may be managed by a microprocessor. The RF system itself may be part of a larger electronic device with the expectation of providing further functionality that is correlated with the RF system.
The bottom line is that RF signals are much less likely to “stand alone” in modern electronics systems. Since the traditional spectrum analyzer only has a single input channel, dedicated to making simple RF measurements, it cannot acquire the complete of set of signals for the embedded design (RF, analog, digital).
The MDO can provide a full complement of input channels:
- 4 analog time-domain channels with 200 MHz, 350 MHz, 500 MHz or 1 GHz of bandwidth with serial bus decode and triggering capability
- 16 digital time-domain channels with up to 60.6 ps timing resolution with serial bus decode and triggering capability
- 1 spectrum analyzer channel with either a 3 GHz or a 6 GHz input frequency range
More importantly, these input channels are all time-correlated. The MDO can show the timing relationships between, say, the serial data command to an RF transmitter and the resultant RF burst. Understanding the relationships between multiple signals within an electronic system is the key to understanding or troubleshooting the behavior of that device.
While this multi-channel view of the world is familiar to oscilloscope users, the mixed domain oscilloscope represents the first time the multi-channel benefits are easily available to spectrum analyzer users.

Concurrent Time and Frequency Views of RF Signals
With the ability to see both the time domain and frequency domain of a time-varying signal, it is much easier to understand the true nature of signal behavior. Simple events signals such as a frequency-hopping signal are very difficult to understand using a traditional spectrum analyzer. The advantage of the MDO architecture can be demonstrated with this example.
The traditional spectrum analyzer will sweep across a defined spectrum. In the example in Figure 7, a traditional spectrum analyzer is set to sweep across 20 MHz of spectrum with a 20 kHz RBW. The sweep duration of the spectrum analyzer defaults to 146 ms at these settings. With the Max Hold Trace (Blue Trace) and Normal Trace (Yellow Trace), it is difficult to understand the time-domain behavior of the signal from the accumulated or instantaneous spectrum view. The only way to view the time domain behavior of this signal using a the traditional spectrum analyzer would be to use the Zero Span mode; however, the bandwidth in the Zero Span mode of the spectrum analyzer is limited to the maximum RBW. Since this signal clearly has spectrum behavior beyond the typical RBW limit of a spectrum analyzer (10 MHz), it would not be useful to see this type of signal on a traditional spectrum analyzer in Zero Span. Also, when the Zero Span mode is selected in a traditional spectrum analyzer, the spectrum view of the signal is no longer available
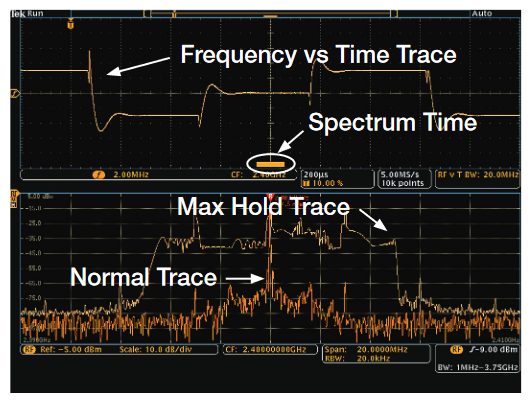
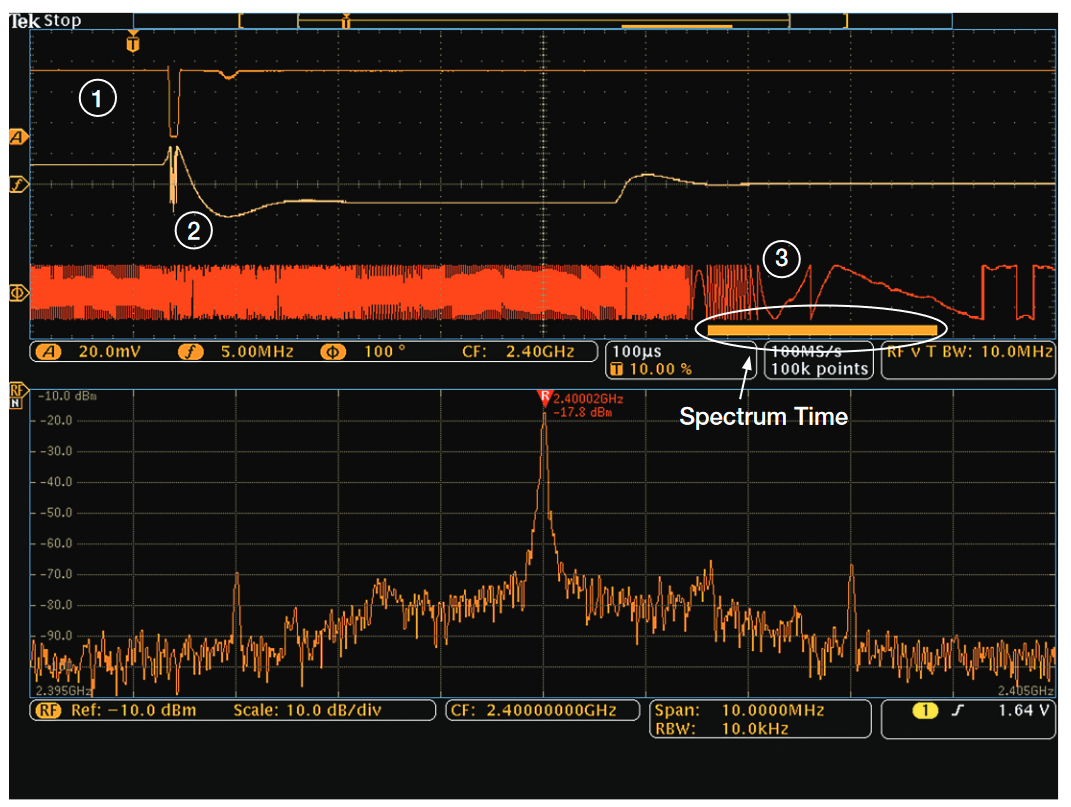
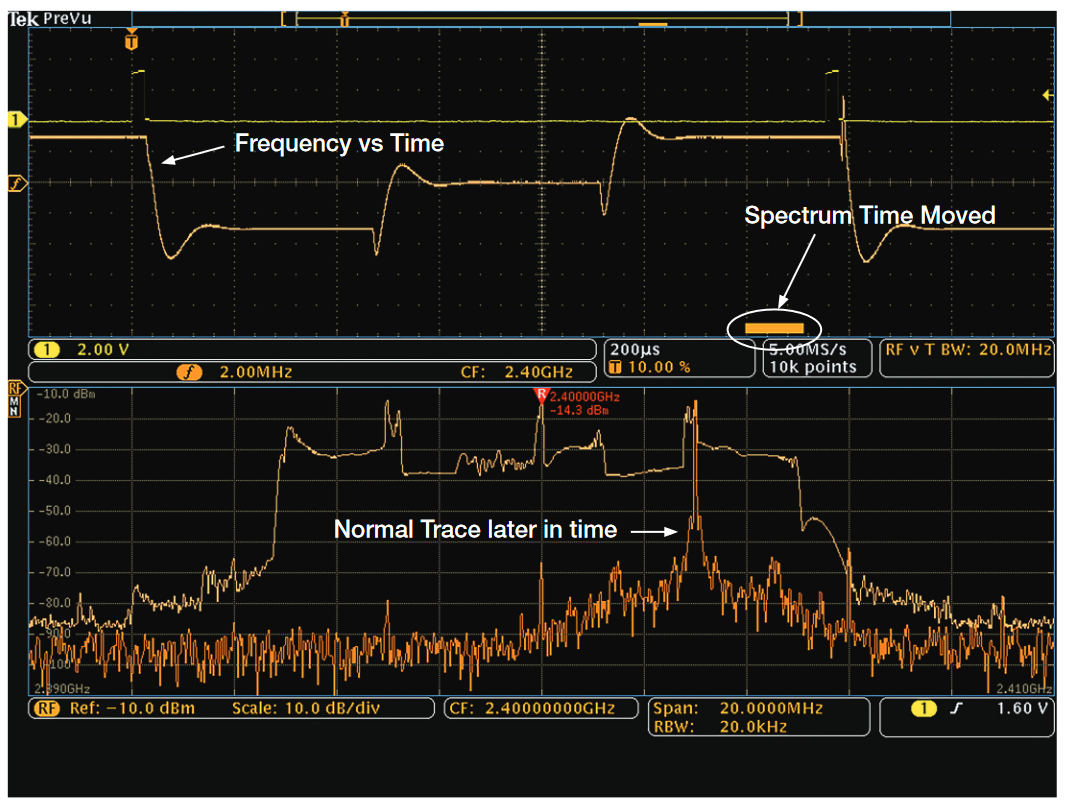
Figure 8 is the same signal now viewed with both the Timeand Frequency-Domain Displays on the MDO4000C. With the Max Hold and Normal Trace displayed, it now becomes obvious that this signal may not be as chaotic as viewed with a traditional spectrum analyzer. The Normal Trace shows the FFT of the signal correlated to the Spectrum Time shown in the Time Domain display (Spectrum Time will be discussed in detail later in the Time and Frequency Domain Correlation section). At the RBW setting of the Spectrum Analyzer, the acquisition time required to display this signal is called the Spectrum Time. This acquisition time is less than 115 µs representing the same bandwidth of the signal in Figure 7, but with a signal acquisition over 1300 times faster.
Understanding the concurrent time and frequency view of RF signals provides the necessary insight to understanding modern signal behavior and proper measurement setup. This example will be discussed in detail during the overview of the spectrum analyzer architectures.
Views of RF signals versus Time
The traditional spectrum analyzer time-domain view can only provide the analysis of signal amplitude versus time (Zero Span), and as previously mentioned the traditional spectrum analyzer cannot display the spectrum and time-domain views of a signal concurrently. Further, frequency and phase versus time are not capable of readily being displayed in a traditional spectrum analyzer. Given these limitations, the benefits of the MDO will be compared to a traditional spectrum analyzer for viewing a pulsed signal using a relatively repetitive signal that does not vary with frequency
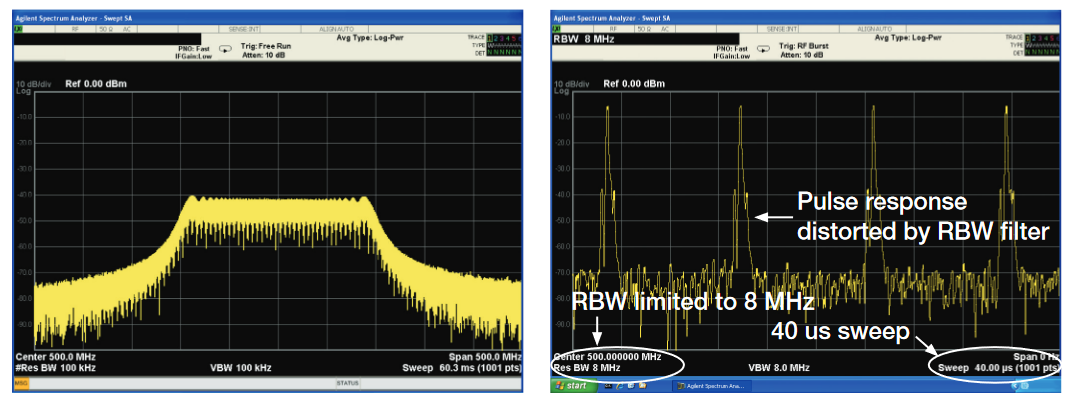
Figure 9 (a/b) shows the spectrum and zero span view of a pulsed signal. The Zero Span display in Figure 9(b) shows the time-varying nature of the amplitude versus time. The signal appears to be some type of pulsed energy with a duty cycle approximately every 10 us.
The Zero Span mode of a traditional spectrum analyzer best represents the time-domain view of the signal when the RBW is set to the maximum of the spectrum analyzer. If the signal risetime is faster than the risetime of the RBW filter the amplitude versus time display will show a distorted representation of the signal.
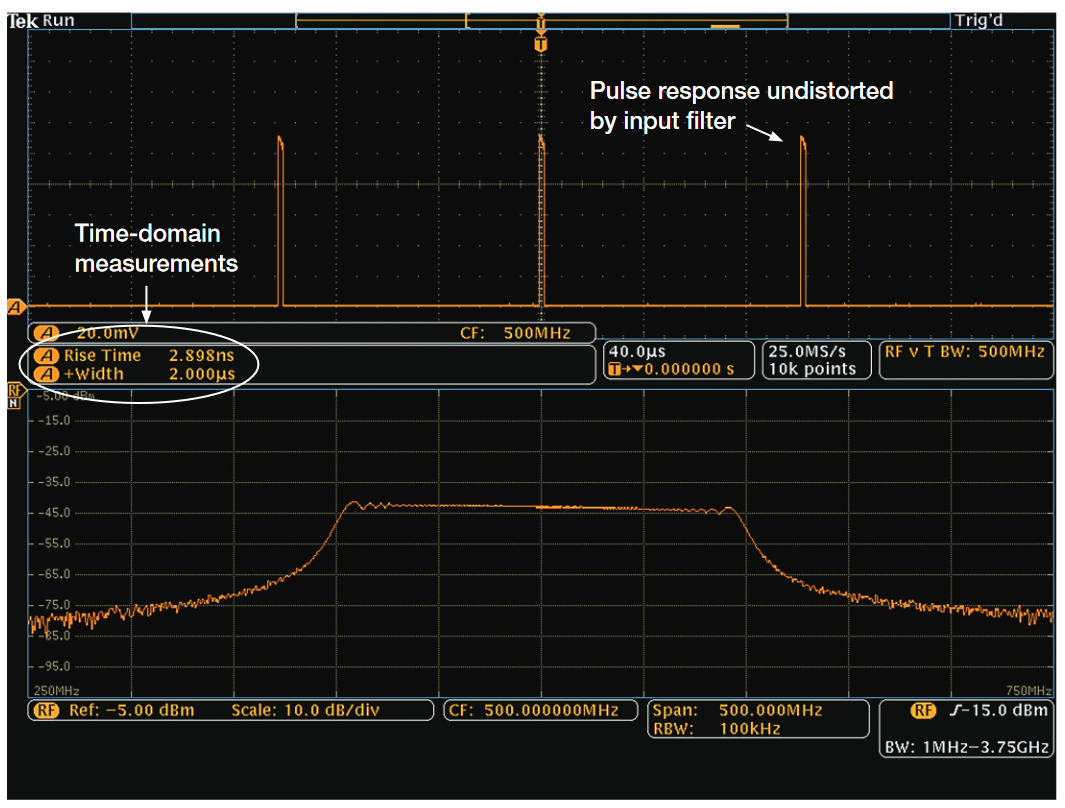
Figure 10 shows the same signal viewed in Time and Frequency displays concurrently on the MDO4000C. Notice the amplitude versus time waveform and automatic measurements that are readily visible in the Time Domain display. When you compare the Amplitude vs Time trace in Figure 10 to the Zero Span display of the traditional spectrum analyzer Figure 9(b), the distortion of the signal caused by the limitations of the RBW are readily apparent. The signal risetime of 2.898 ns and the pulse duration of 2 us are reported in the measurement display for the Amplitude versus Time trace.
The limited bandwidth and RBW of the traditional spectrum analyzer will not allow the risetime to be accurately displayed or measured. The MDO not only provides the ability to view the RF signals versus time (Amplitude, Phase, and Frequency), but the architecture will not distort the signals like a traditional spectrum analyzer because the time-domain views are not limited by the RBW settings of the instrument.
Time-Based Wide Capture Bandwidth Acquisition
The spectrum analyzer was first developed in an era when frequency-domain analysis was done on RF signals that were stable over time and had simple narrowband modulation schemes, like AM or FM. Signals used in today's digital communications, however, vary significantly with time, using sophisticated digital modulation schemes and, often, transmission techniques that involve bursts of RF. These modulation schemes can be very wide bandwidth as well.
In order to address the bandwidth requirements of modern measurements, the MDO4000C provides a minimum of 1 GHz of capture bandwidth. At span settings of 1 GHz and below, there is no requirement to “sweep” the display. The spectrum is generated from a single acquisition, whose timespan is defined by the RBW setting. A traditional swept analyzer, or a narrow-band FFT analyzer, will take a significant amount of time (the sweep time) to capture the range of frequencies associated with the span. For example:
With settings of 40 MHz span, 30 kHz RBW:
- MDO4000C spectrum time: 74.3 µs
- Typical spectrum analyzer sweep time: 116.4 ms5
As can be seen, the MDO4000C is able to acquire the necessary data over 1000X faster than the spectrum analyzer. This provides much better insight into the spectral content of a fast changing signal at a specific point in time.
A traditional swept analyzer can be made to sweep faster, but it suffers from amplitude or phase shift as the sweep speed is increased. In contrast, the MDO4000C will capture an entire span of data in the minimum possible amount of time without distortion. Increasing the RBW setting directly reduces the timespan of the acquisition data. This relationship will be discussed in the Time and Frequency Domain Correlation in the next section.
For more information on these relationships, see the section on Acquiring the Raw RF Time Domain Data Record
In order to deal with the time-varying nature of these modern applications, the MDO provides a triggered acquisition system that is fully integrated with the time-domain channels. This allows the user to capture a spectrum at precisely the point in time where an interesting frequency-domain event is occurring
It should be noted that triggering can be disabled for spectrum traces, if desired. This can be useful when the frequency-domain data is continuous and unrelated to events occurring in the time-domain.
The MDO4000C: Powerful Combination of Capabilities
As noted above, the MDO4000C provides a unique combination of capabilities. These capabilities are highlighted in this section.
It should be noted that the capabilities highlighted here are in addition to the full complement of time-domain measurement capabilities found on the MSO4000C Series Mixed Signal Oscilloscope.
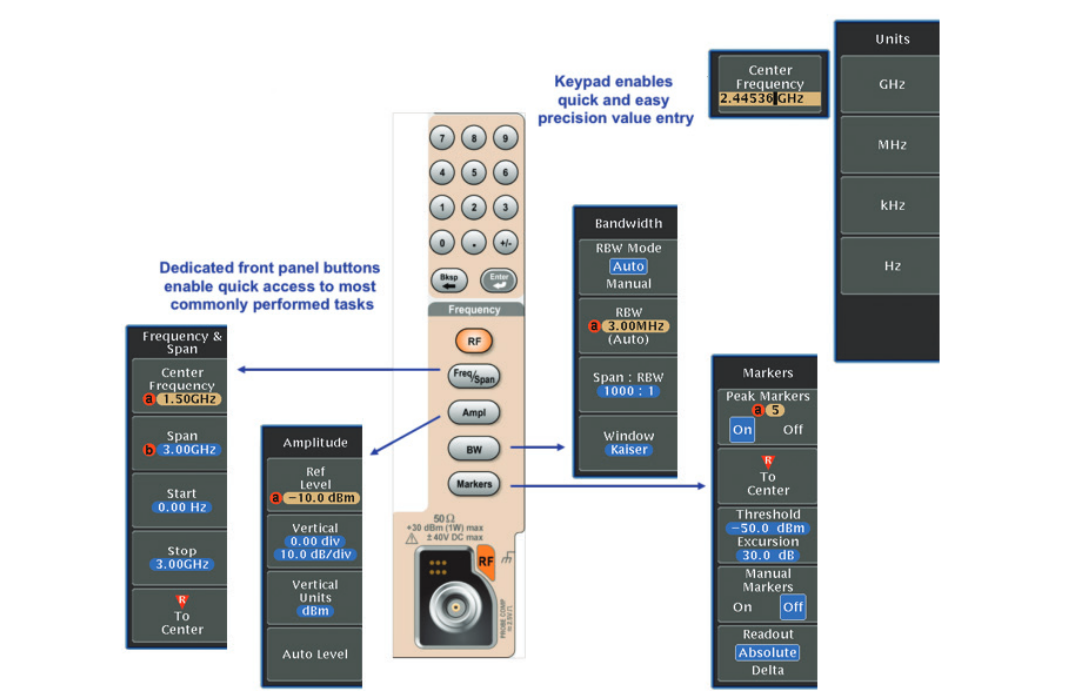
Dedicated Spectral User Interface
Unlike any other scope-based spectral analysis tool, the MDO provides dedicated front panel controls and an optimized menu structure for making spectral measurements:
Front panel buttons provide direct access to the following menus:
- RF; for turning traces on, controlling the spectrogram display, and defining the detection method.
- Freq/Span; for defining the center frequency and span or the start and stop frequencies of the spectrum display.
- Ampl; for setting the reference level, the vertical scale and position, and the vertical units of the spectrum display.
- BW; for setting the resolution bandwidth and the FFT window type.
- Markers; for turning on both peak and manual markers, changing between relative and absolute marker readouts, moving the reference marker to center, and defining the vertical levels that define a peak.
In addition, a numeric keypad allows easy entry of precise values.
The display automatically manages a time-domain and a frequency-domain window as needed. RF time-domain data is displayed in the time domain window, along with other time-domain data from the analog or digital channels. Spectral data is always displayed in an independent frequency-domain window.
The following elements are illustrated in this screen shot:

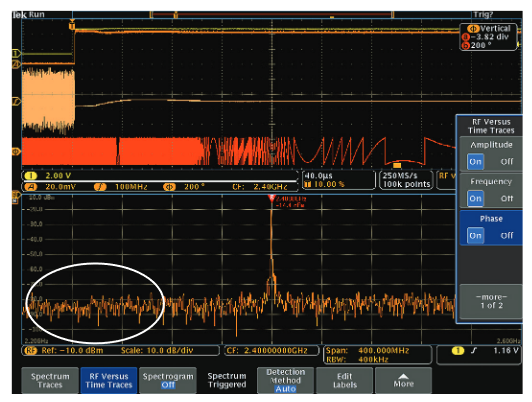
1. Time-domain traces: “Normal” oscilloscope traces. In this case, the Yellow Trace (Channel 1) is the signal controlling the frequency hop (used as the trigger source) and the Blue Trace (Channel 2) is the SPI serial bus data changing the oscillator frequency.
2. RF time-domain trace: A specialized time-domain trace, derived from the spectrum analyzer input, which allows the user to view the amplitude, phase, or frequency of the RF signal as a function of time. The orange trace “f” shows the Frequency versus Time on a 2.00 MHz/division scale. All of the RF time-domain traces are derived from the time-domain IQ data acquired by the spectrum analyzer. They are time-correlated with the other analog and digital channels and represent a continuous time-domain data stream. For more information on how these RF time-domain traces are calculated and displayed, see Generating RF Time-Domain Data.
3. Spectrum trace: A typical spectrum analyzer trace. Like a traditional spectrum analyzers trace, different trace types can be viewed: Max Hold, Average, Normal, and Min Hold. See Spectrum Traces, section for more information
4. Spectrum time indicator: An indication of where in time the spectrum analyzer acquisition occurred. The trace is derived from a time sampled acquisition that is correlated with the other analog and digital channels, and represents a continuous time-domain data stream.
5. Peak markers: Automatic frequency and amplitude readouts for peaks. See Markers section for more information.
6. Frequency-domain settings: Readouts of critical frequencydomain parameters, including Ref Level, Center Frequency, Span, and RBW settings.
7. Trigger settings: Readouts of critical trigger parameters. See the Triggering, section for more information.
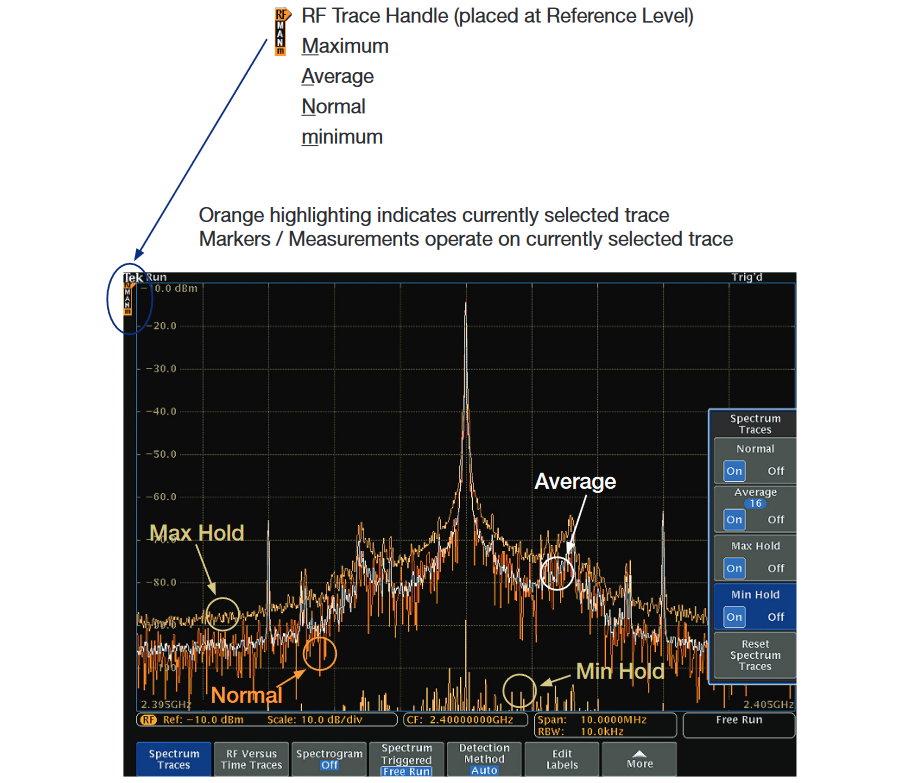
Spectrum Traces
The frequency-domain window provides support for four spectrum traces. They include:
Normal: a “Normal” trace is replaced with each new acquisition
Average: an “Average” trace represents an average of the last N “Normal” traces.
Max Hold; the maximum data values found in the “Normal” trace accumulated over multiple acquisitions
Min Hold; the minimum data values found in the “Normal” trace accumulated over multiple acquisitions
Each of these traces may be turned on and off independently, and all four may be displayed simultaneously.
Figure 13 shows the four traces measuring a CW signal. The Markers and Measurements can be referenced to any trace, so the RF Trace Handle is used to indicate the trace reference.
The Max Hold, Min Hold, and Average traces are automatically reset when acquisition parameters are changed. This eliminates confusing displays that are the composite of traces taken with different acquisition settings.
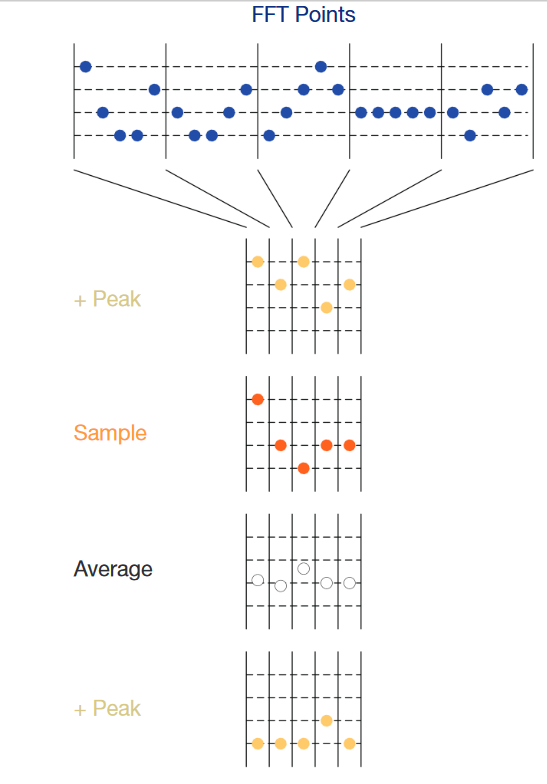
Detectors
Detectors play an important part in the analysis and measurements of the input signal and the creation of traces. There are four basic methods of detection: + Peak, Average, Sample, and – Peak. Unlike a traditional spectrum analyzer, the MDO spectrum trace is calculated using an FFT of time sampled data. There are two types of decimation typically employed by vector signal analyzers. Decimation of sample rate to keep just enough sample points to support the required span, and decimation of FFT data to remove excess data that can clutter the display. Since the FFT size can be as much as 2,000,000 points, the MDO4000C uses a process to reduce, or decimate, the sampled data before the FFT is calculated.
The MDO will perform FFTs ranging from 1,000 points to ~ 2,000,000 points depending upon acquisition settings for span and resolution bandwidth. The Detection Methods are used to determine how to compress the 1000-2,000,000 point FFT output to a 1,000 pixel wide display. The decimation factor determines how many sample points of data are used in each group of data compression. The compression works as follows:
+ Peak – uses the highest amplitude point in a set of FFT data
Sample – uses the first point in each group
Average – averages all points in a group
- Peak – uses the lowest amplitude point in a set of FFT data
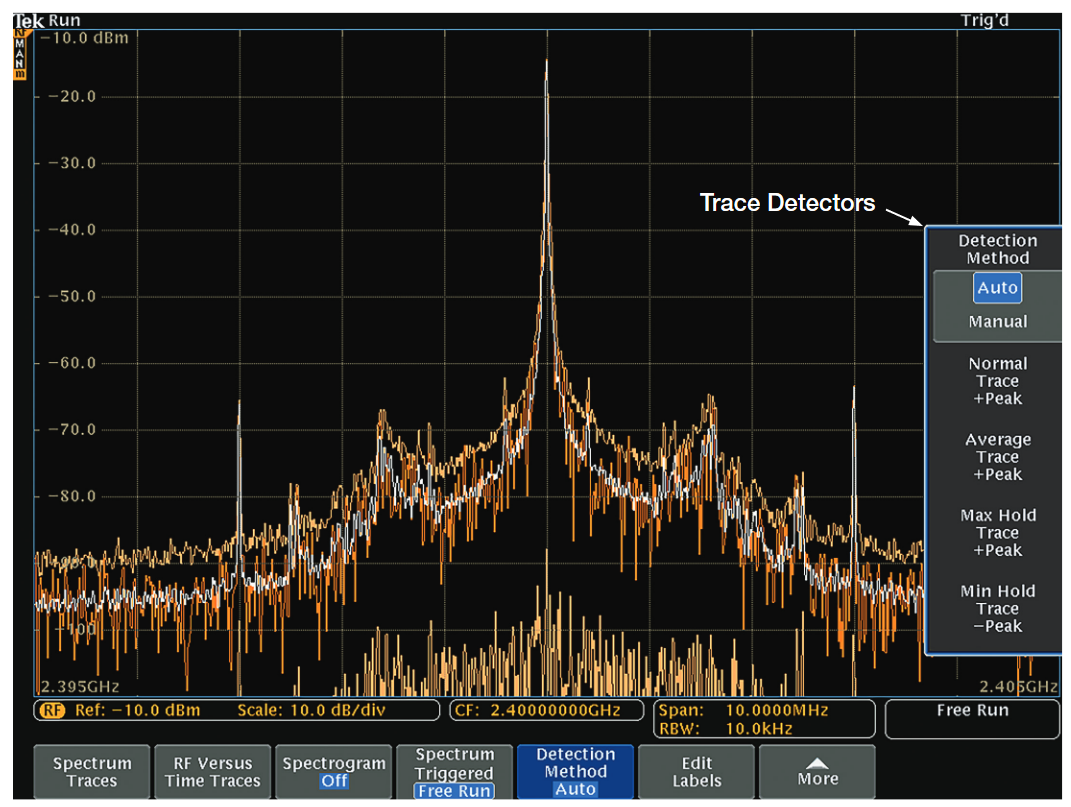
While the MDO4000B provides flexibility for manual control of the Detection Method, it should be noted that there are defaults set for each trace depending on whether RF Measurements (See RF Measurement section for more detail) are ON or OFF
When RF Measurements are OFF, the default detectors for each trace are as follows:
- Normal: +Peak
- Average: +Peak
- Max Hold: +Peak
- Min Hold: -Peak
When RF Measurements are ON, the default detectors for each trace are as follows:
- Normal: Average
- Average: Average
- Max Hold: Average
- Min Hold: Average
In all cases, manual control is available if the user desires.
RF Time-Domain Traces
In addition to all the usual analog and digital channels, the time domain window provides support for three RF timedomain traces. These traces, derived from the underlying IQ data of the spectrum analyzer input, allow analysis of critical parameters of the RF signal. They include:
- Amplitude: the instantaneous amplitude of the input signal after band-pass filtering to the current frequency range, as defined by the center frequency and span settings
- Frequency: the instantaneous frequency of the input, relative to the center frequency
- Phase: the instantaneous phase of the input signal. The reference for phase measurements is a hypothetical signal at the center frequency.
Each of these traces may be turned on and off independently, and all three may be displayed simultaneously.
The following traces are shown in Figure 16 (a frequencyhopping signal with frequency ringing):
1. The Amplitude vs. Time trace: Notice that the amplitude is essentially unchanged as the signal hops between frequencies.
2. The Frequency vs. Time trace: The vertical axis is frequency, relative to the center frequency. The signal is hopping between a frequency that is lower than the center frequency (signal at the left edge of the screen) to one that is roughly at the center frequency, to one that is higher than the center frequency. Notice that the severe frequency ringing as the signal hops between frequencies can be easily seen with this trace.
3. The Phase vs. Time trace: The vertical axis is phase, with wrapping at roughly +/- 180°. Notice that there is a slight mismatch between the middle frequency hop and the center frequency thus, during that hop, the phase relative to CF is changing slowly. For analyzing phase versus time, it is best to use a phase lock reference between the device under test and the MDO. During the remaining hops, the frequency mismatch is so large that the phase change appears as a solid band.
All of these traces are derived from the time-domain IQ data acquired from the spectrum analyzer input. They are timecorrelated with the other analog and digital channels and represent a continuous time-domain data stream.
For more information on how these RF time-domain traces are calculated and displayed, see Generating RF Time-Domain Data.

Time- and Frequency-Domain Correlation
As noted previously, all time- and frequency-domain data is time-correlated. All analog channels, digital channels, and RF time-domain traces are shown together in the upper time-domain window. As with any Tektronix MSO/ Series oscilloscope, the traces are time-correlated and can be analyzed with Wave Inspector, multipurpose markers, measurements, cursors, etc.
A new indicator has been added to the display to indicate the location, in time, of the data that is being used to generate the spectrum display. This Orange Bar, called the Spectrum Time Indicator, can be seen at the bottom of the time-domain window in Figure 17.
As can be seen by the frequency vs. time trace, (the Orange Trace, “f”, in the time-domain window), this is a frequency hopping signal.
The frequency ringing as the signal transitions from one frequency to the next is clearly visible in both the frequency vs. time display and the spectrum display. This is highlighted by the two circled trace segments.
Over the spectrum time (shown by the Orange Bar), the signal is at the middle frequency for the most time. This can be seen at 1. This results in a high amplitude peak at 4.
The signal is at the highest frequency for the least amount of time (due to ringing). This can be seen at 2. This results in a low amplitude peak (not visible above the ringing) at 5.
The signal is at the lowest frequency for a modest amount of time. This can be seen at 3. This results in a modest amplitude peak at 6. Notice also, that no ringing is reflected at this frequency. This is due to the signal being stable as it enters the spectrum time interval. The ringing associated with the mid-to-high frequency transition is outside of the spectrum time.
When you compare Figure 16 to Figure 17, notice that the timebase is now 10 times faster in Figure 17 (2 ms to 200 us per division). This is a frequency-hopping signal that is much faster. In Figure 17, the RBW is now 2 kHz and the Spectrum Time is longer than a single dwell time on any one frequency. In order to see the spectrum of a single hop, it would be necessary to shorten the acquisition time with a wider resolution bandwidth.
The Wave Inspector knobs control the position of Spectrum Time (indicated by the orange bar) relative to the other timedomain traces:
- The default location for Spectrum Time is centered in the time-domain window
- When zoom is on, Spectrum Time follows the zoom window
- When zoom is off, as in the above illustration, the pan knob can be used to move the relative position of Spectrum Time
The Spectrum Time indicator is helpful in making accurate power measurements on transient and short duration RF signals. By ensuring that the signal is stable over the entire spectrum time, the amplitudes shown in the spectrum display will be accurate. This condition can be easily verified in the time-domain window.
A more detailed explanation of the relationship of RBW and FFT Windowing is presented in Appendix A: Windowing Functions of this application note.
Triggering
Because of the integration of the spectrum analyzer into the time-domain-based acquisition system in the MDO4000C, the acquisition process can be triggered. In the previous example, the frequency-hopping signal is stable on the display because it is being triggered by the control signal for the hop (the narrow pulse on the Yellow Trace, CH1.
The spectrum analyzer options add the following capabilities to the MDO4000C Series trigger system:
- The ability to edge trigger on the overall power level on the spectrum analyzer input, after the block downconversion (see Block Downconversion, below, for more details).
Timeout
- Sequence (B Trigger)
- Pulse Width
- Runt
- Logic, in combination with other analog and digital inputs
Spectrogram
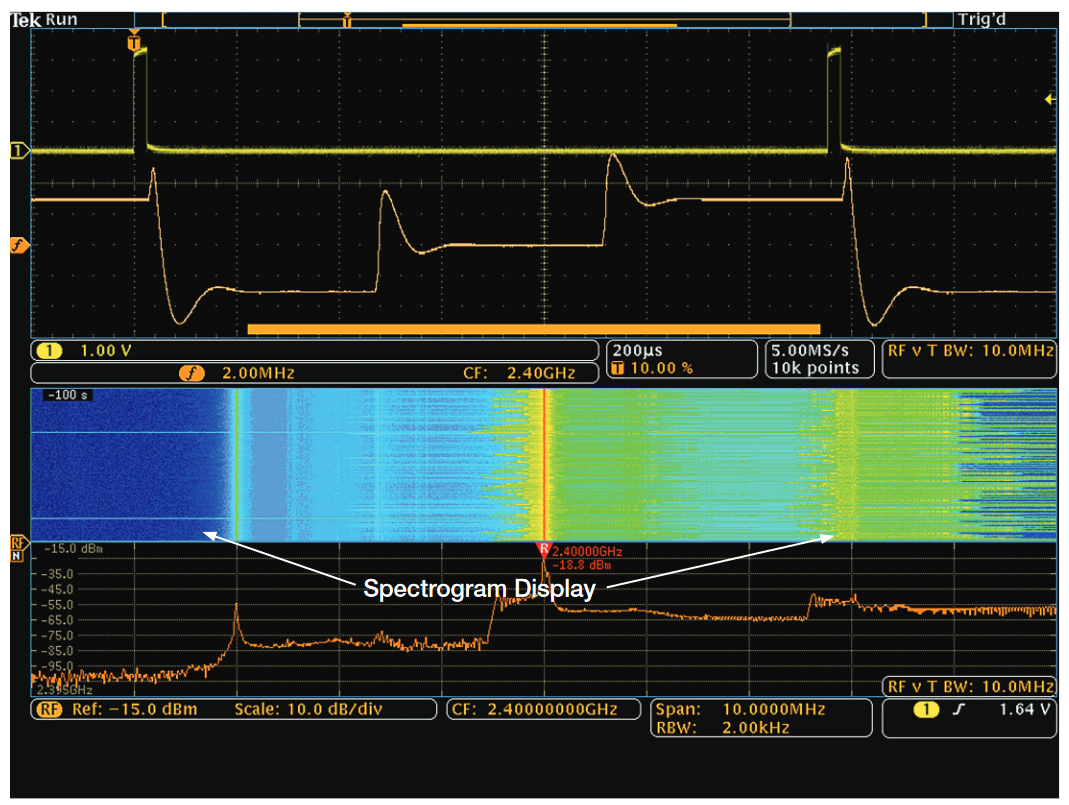
The MDO4000C provides a spectrogram display. This display can provide valuable insight into RF signals that are changing in frequency at a relatively slow rate.
The spectrogram is a series of spectrum traces tipped “on end” by encoding the magnitude of the signal with color. An individual “slice,” then, is blue where the signal amplitude is low, changing color to red where the signal is high amplitude. These slices are then stacked vertically, with the newest
spectrum at the bottom of the spectrogram. See Generating the Spectrogram, for more information on how this display is generated.
The spectrogram display is illustrated in Figure 18.
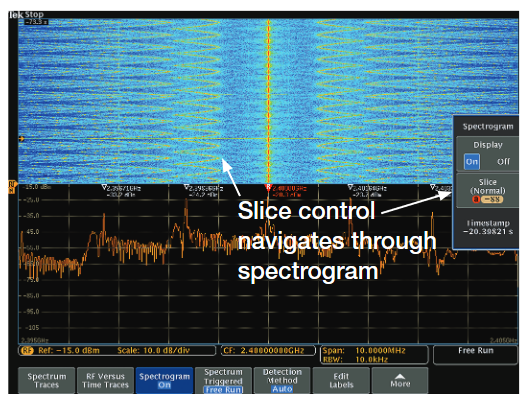
Notice how clearly the frequency-hopping nature of the signal is communicated, even though no single spectrum trace shows all of the hop frequencies. Once an acquisition is stopped, the previous spectrums can be viewed by scrolling through the history of captured data.
Markers
The MDO4000C leverages the best paradigms of both spectrum analyzers and oscilloscopes with its implementation of markers in the frequency-domain window.
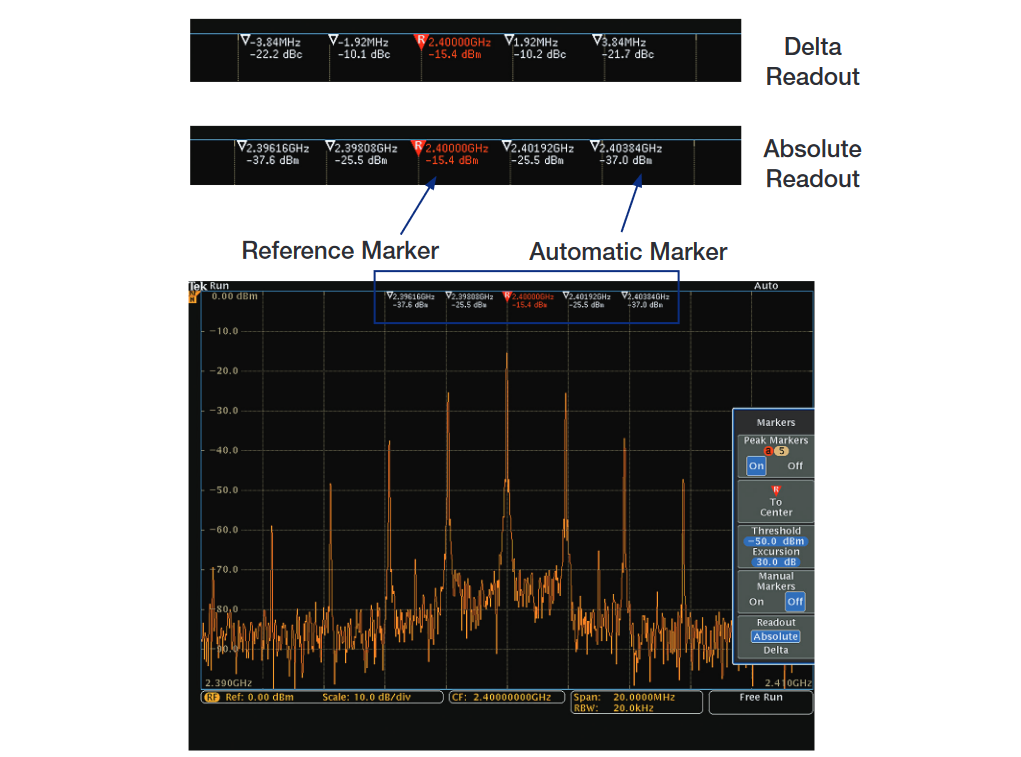
The powerful search capability of the Tektronix MSO/DPO Series oscilloscopes is leveraged to provide an automatic Peak Marker capability. This capability is turned on by default and not only automatically identifies the single highest peak, but up to 10 additional peaks that meet user specified criteria. This is illustrated in Figure 19.
The “reference marker” is automatically set to the highest peak. The reference marker is shown in red in Figure 19, and the next markers are automatically set to the next highest peaks, up to a user-set maximum of 11 markers.
The peak readouts can be set to either absolute or delta (relative). When set to relative, they are measured relative to the reference marker.
Compare this to the operation of a typical spectrum analyzer to provide the same data:
- Turn on a marker
- Use marker to peak navigation controls, if available, to navigate to the appropriate peak
- Repeat with additional markers
Note also, that the peak markers continuously and automatically update. If the signal is changing in frequency, the peak markers stay attached to the peaks. This is similar to the tracking function found on some spectrum analyzers, but applies to all peak markers simultaneously.
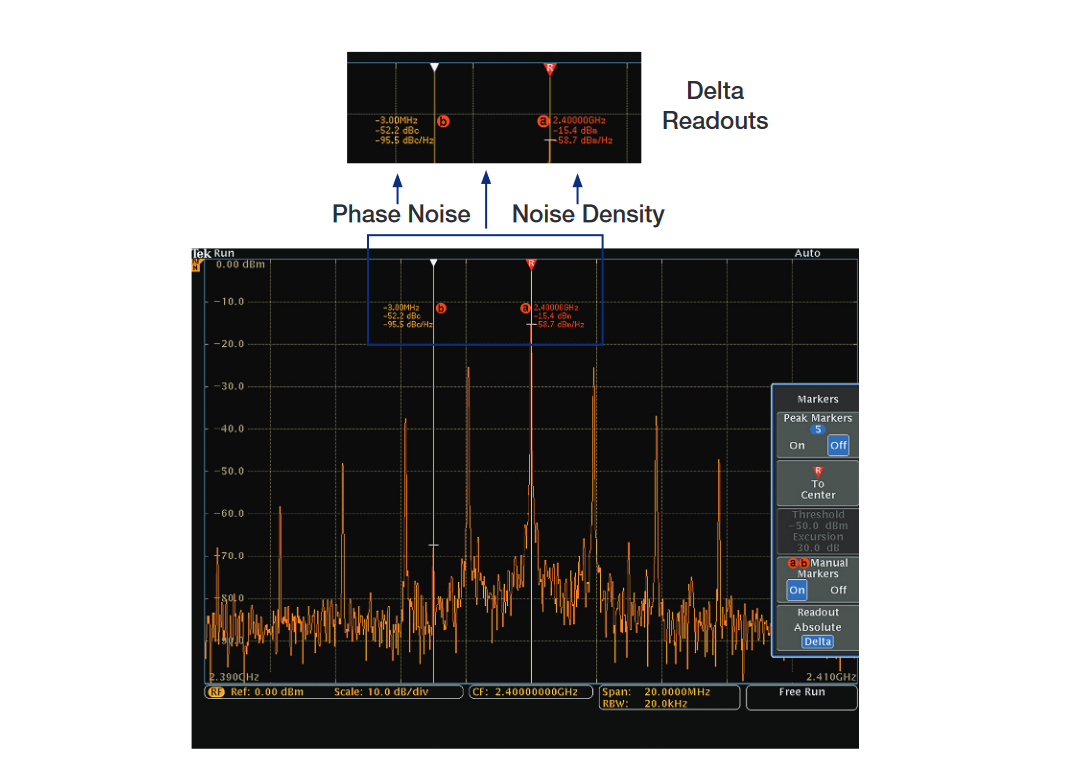
The addition of manual markers allows the user to manually measure spectral content away from signal peaks. This capability is illustrated in Figure 20.
Notice that two manual markers have been turned on. The reference marker is automatically changed to the a marker.
As with peak markers, the manual markers can read out either absolute or delta data. They are set to delta in this screen shot.
In addition, both the a and b markers provide spectral density readouts for making noise density measurements (with absolute readouts) and phase noise measurements (with delta readouts).
A Marker to Center function is provided to adjust the center frequency to bring the reference marker to the center of the screen.
RF Measurements
A number of specialized RF measurements are supported. These include Channel Power, Adjacent Channel Power Ratio, and Occupied Bandwidth measurements.
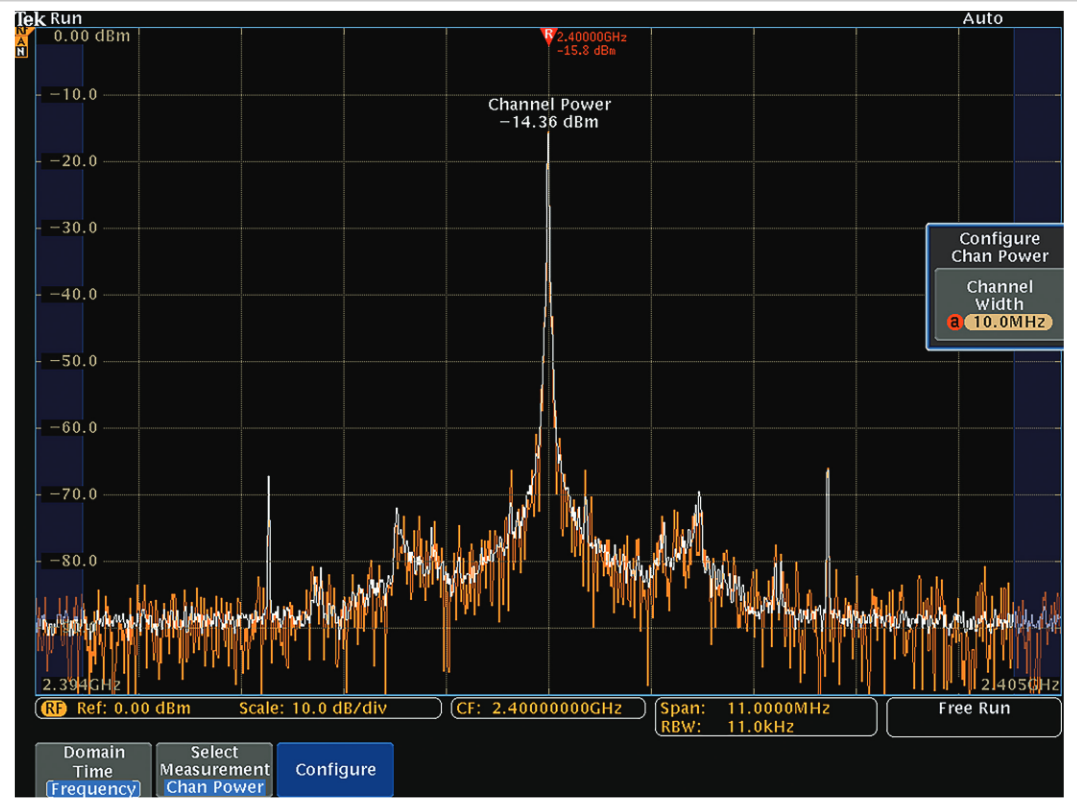
Channel Power
Channel Power provides the ability to measure the total power within a user defined bandwidth. The Channel Width is indicated by the non-shaded portion of the display in Figure 21. When the measurement is active, the Span is automatically set to 10% wider than the Channel Width.
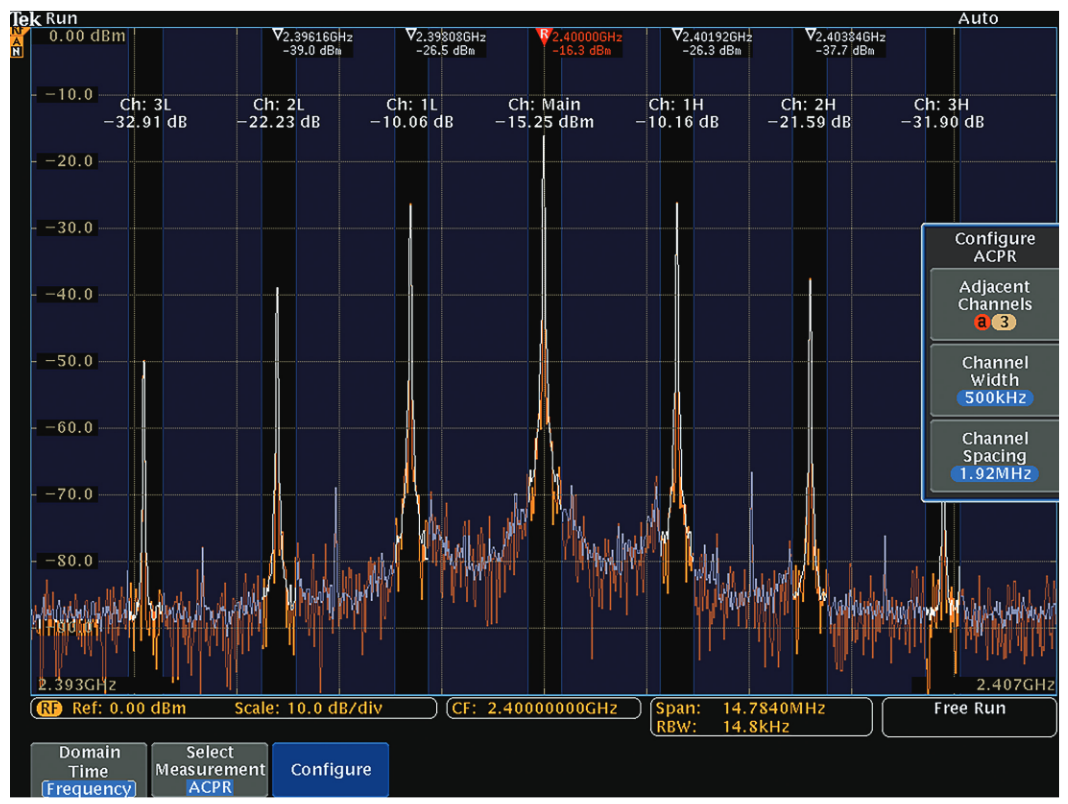
Adjacent Channel Power Ratio
The Adjacent Channel Power Ratio (ACPR) measurement returns the power in the main channel and the ratio of channel power to main power for the upper and lower channels adjacent to the main channel.
Channels can be user defined and are indicated by the non-shaded portions of the display. When this measurement is active, the Span is automatically set 10% larger than the required span to capture all channels.
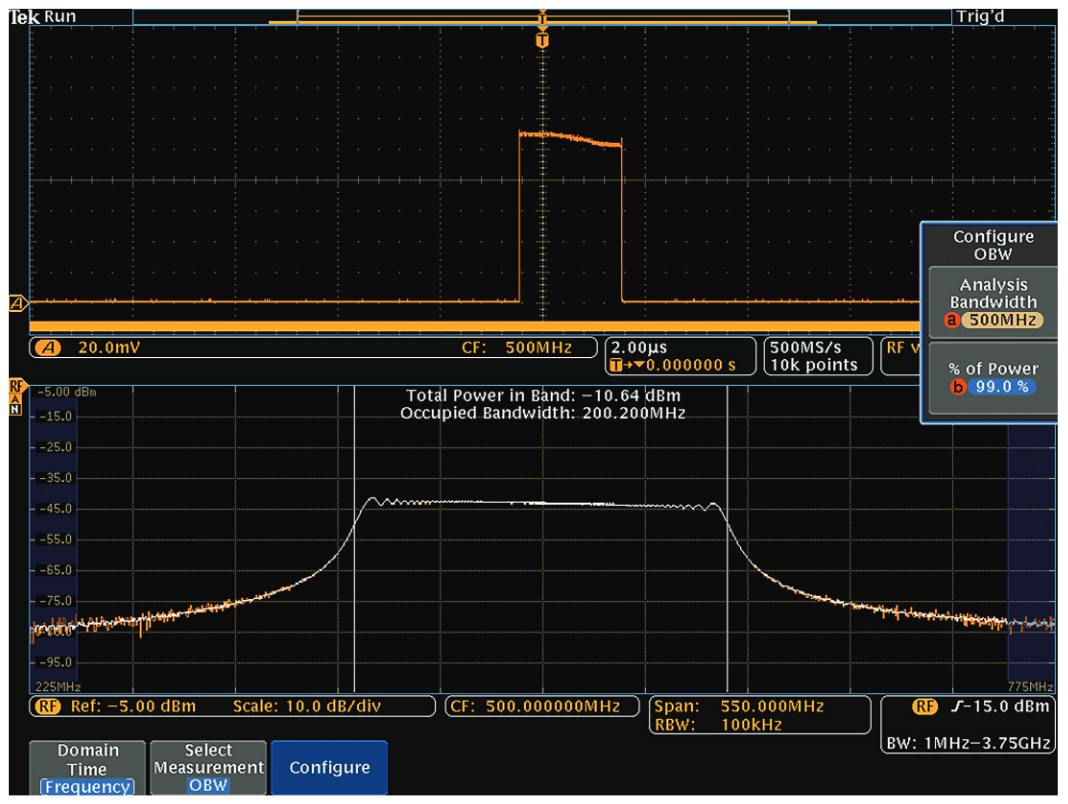
Occupied Bandwidth
The Occupied Bandwidth, or OBW measurement, provides the ability to measure the bandwidth that contains a specified percentage of the power within a user defined analysis bandwidth.
When the OBW measurement is active, the Span is automatically set 10% wider than the Analysis Bandwidth, and the Analysis Bandwidth is indicated by the non-shaded portion of the spectrum display.

Clipping Indicator
Because the display on a spectrum analyzer shows the power level at multiple frequencies, it is difficult to tell when the acquisition system is clipping and, therefore, causing distortion. Looking for peaks above the reference level is insufficient to detect this condition, as each peak contains only a portion of the power seen by the A/D converter. Together, multiple peaks may cause the A/D to clip even if none of the individual peaks exceed the reference level.
Because of the oscilloscope-based acquisition architecture of the MDO4000C, a clipping indicator can easily be provided on the spectrum analyzer input. The instrument looks for any clipping at the A/D converter and signals possible distortion when it is detected.
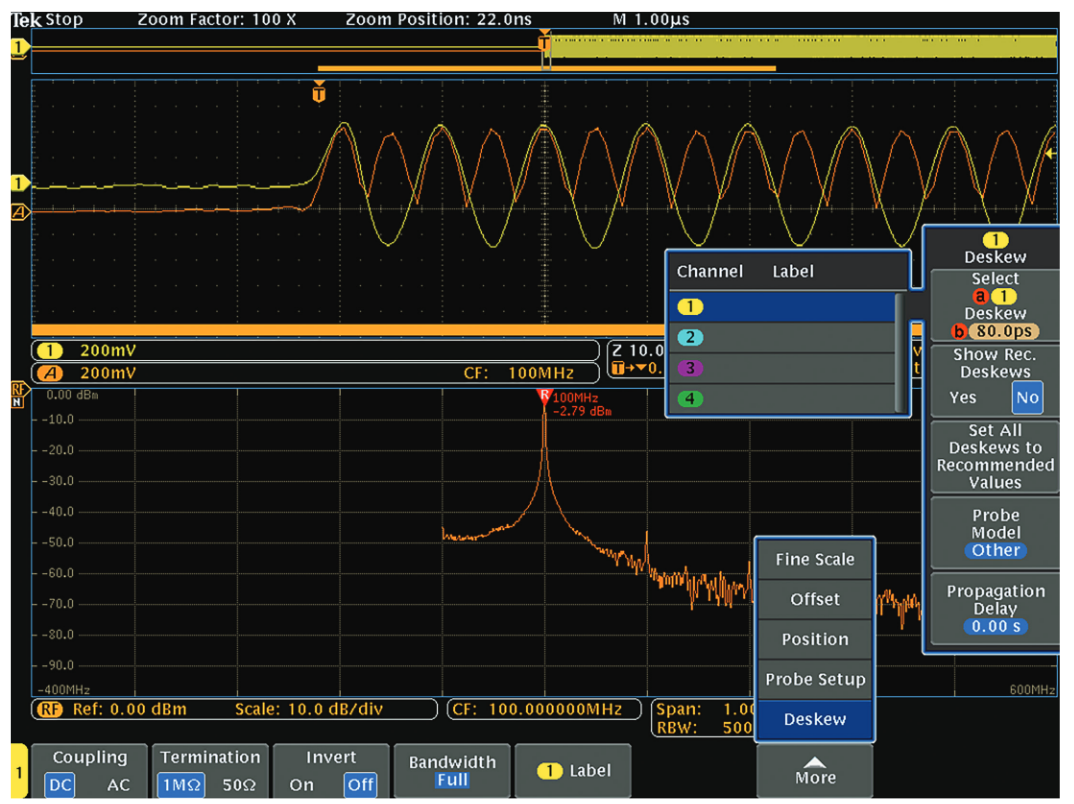
RF to Analog Channel Alignment
While the RF to Analog Channel Skew is specified to be less than 5 ns, the MDO4000C allows the user to perform a deskew adjustment between the RF and any analog channel for more precise alignment.
Chapter 3: Under the Hood
In order to provide the capabilities described above, the MDO4000C mixed domain oscilloscope has a unique architecture that may be unfamiliar to users of traditional spectrum analyzers or oscilloscopes. This chapter explores the technical underpinnings of the MDO4000C.
Spectral Analysis Basics
As shown in Figure 26, signals can be viewed in either the time domain or the frequency domain:
In the time domain, traditional for an oscilloscope, signals are viewed as amplitude vs. time. In the frequency domain, traditional for a spectrum analyzer, signals are viewed as amplitude vs. frequency. In spectrum analyzers, Zero Span mode, the amplitude vs. time of a signal can be displayed where amplitude is defined as the maximum height of a sine wave.
As can be seen, the signal is the same in both cases. A time-domain signal is simply a composite of a number of discrete sine waves, each with their own amplitude and relative phase. The “spectrum” that is shown in a spectrum analyzer is simply the decomposition of the signal into its constituent frequency components.

A simplified block diagram of a traditional swept spectrum analyzer is shown in Figure 27(a).
The swept tuned, superheterodyne spectrum analyzer is the traditional architecture that first enabled engineers to make frequency-domain measurements several decades ago. Originally built with purely analog components, the SA has since evolved along with the applications that it serves. Current generation SAs include digital elements such as ADCs, DSPs, and microprocessors. However, the basic swept approach remains largely the same and is best suited for observing controlled, static signals. The SA makes power vs. frequency measurements by downconverting the signal of interest and sweeping it through the passband of a resolution bandwidth (RBW) filter. The RBW filter is followed by a detector that calculates the amplitude at each frequency point in the selected span. While this method can provide high dynamic range, its disadvantage is that it can only calculate the amplitude data for one frequency point at a time. This approach is based on the assumption that the analyzer can complete at least one sweep without there being significant changes to the signal being measured. Consequently, measurements are only valid for relatively stable, unchanging input signals. If there are rapid changes in the signal, it is statistically probable that some changes will be missed.
These limitations were discussed briefly in an early section of this application note, Concurrent Time & Frequency Views. Figure 7, in that section, discussed the limitations of being able to properly understand a time-varying signal due to the inability to see both time and frequency views at the same time. This section gives more insight to why fast time-varying signals will be viewed differently on traditional spectrum analyzers and vector signal analyzers.
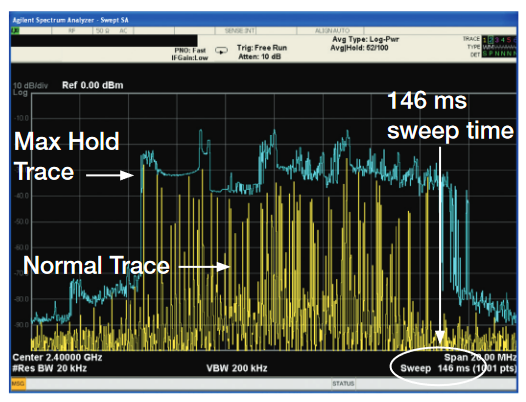
The traditional spectrum analyzer will sweep across a defined spectrum. In the example in Figure 28, a traditional spectrum analyzer is set to sweep across 20 MHz of spectrum with a 20 kHz RBW. With a default sweep duration of 146 ms, the Max Hold Trace (Blue Trace) and Normal Trace (Yellow Trace) are turned on to view the spectrum response.

Figure 29 is the same signal now viewed with both the Time and Frequency Domain Displays on the MDO4000C. With the Max Hold and Normal Trace displayed, the Normal Trace shows a much cleaner looking signal. The Normal Trace shows the FFT of a very brief portion of the time-varying signal. With a 20 kHz RBW, the Spectrum Time is less than 115 µs
The Time Domain display shows Frequency versus Time of this signal represented by the Orange Trace labeled “f”. The frequency scale is set 2.00 MHz per division. A cursory view of the Frequency versus Time display shows this signal appears to hop between three separate frequencies over an approximate 1.4 ms time period. Each frequency appears somewhat stable for approximately 400 us, while the transition between frequencies takes about 100 us. These events are much faster than the sweep time of a traditional swept spectrum analyzer. Over 100 of these sets of events occur during each sweep of the spectrum analyzer based on the settings selected in Figure 28 (146 ms sweep time).
Using the Wave Inspector knob on the front panel of the MDO4000C, the entire time captured can be explored in the frequency domain. Figure 30 is the same captured signal, but now the view of the spectrum display is representative of a different point in time. Spectrum Time has now been moved to the higher frequency of the triple hop sequence of this RF signal, and the spectrum recalculated for this new point in time.

In Figure 31, Spectrum Time is moved to the transition between the highest and lowest frequency in the step sequence. This broad spectrum is clearly seen using a broadband spectrum analyzer; however, it is difficult to resolve using a traditional spectrum analyzer with a narrowband detector sweeping across a spectrum of interest.
For the signal displayed on the traditional swept analyzer in Figure 28, the broad spectrum is represented as an architectural artifact of a swept analyzer when it is slowly swept across a fast moving signal. It was previously determined that over 100 frequency-hopping cycles occurred during the sweep time (146 ms) of the traditional spectrum analyzer. During a single frequency-hopping cycle lasting about 1.4 ms, there are up to three broadband spectrum events due to the three frequency transitions. The narrowband detector of the traditional spectrum analyzer represents the event only as the energy received at the frequency of the detector during the sweep, thus up to 300 noise events in addition to the 300 settled frequency events occur. Looking at the traces in Figure 28, it would not be possible to understand this signal behavior. The noise spikes shown on the spectrum view of the traditional analyzer are not representative of the real broadband noise, they are just an artifact of using the wrong tool to look at a broad spectrum event.
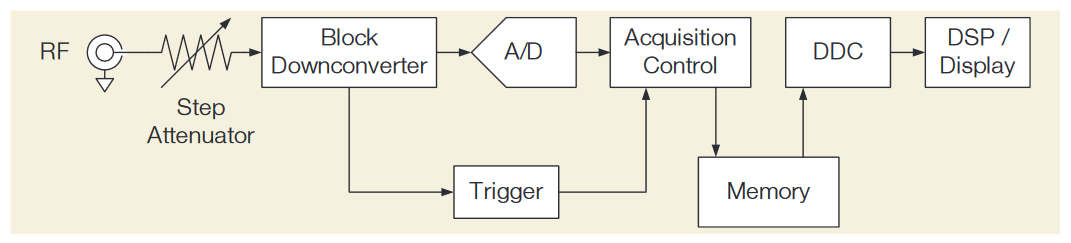
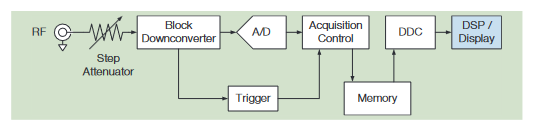
The Vector Signal Analyzer, VSA, architecture is shown in Figure 27(b) and the simplified block diagram of the MDO4000C in Figure 32. Representing a more modern spectrum analyzer, the local oscillator is stepped, rather than swept. The resultant signal is filtered and then digitized. This results in a band-limited time domain signal that can be converted from the time-domain to the frequency domain through the use of a DFT (Discrete Fourier Transform). Of these transforms, the most well-known is the FFT (Fast Fourier Transform). The resultant frequency-domain information is then used to draw a small portion of the spectrum on the display around the frequency of the local oscillator. Then the local oscillator is stepped to the next higher frequency and the process repeats until the full spectrum has been drawn. Stepped analyzers are marginally better than swept analyzers for working with time-varying RF, but only to the extent that the span of interest is within the step width which is usually quite narrow.
This same process of acquiring a signal in the time domain and converting it to the frequency domain through the use of a DFT is at the heart of the spectrum analyzer function in the MDO4000C Series Mixed Domain Oscilloscope.
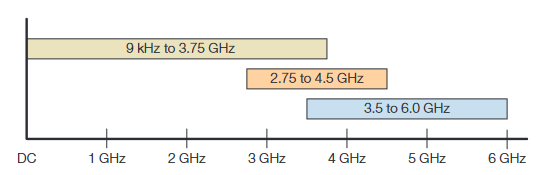
Where the MDO is unique is in its extremely wide acquisition bandwidth and multi-channel time-correlated architecture. Typical stepped spectrum analyzers have capture bandwidths of around 10 MHz. The MDO4000C Series has a minimum capture bandwidth of 1 GHz at all center frequencies and as much as 3.75 GHz in some cases
A simplified block diagram of the spectrum analyzer in the MDO4000C is shown in Figure 32.
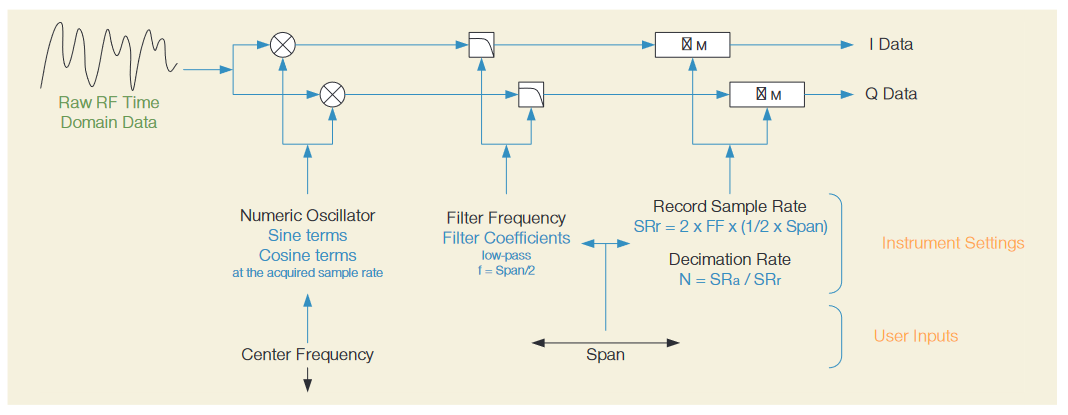
Rather than sweeping or stepping across the frequency range of interest, a wide-bandwidth block downconverter is used to feed a high sample rate A/D.
A wide bandwidth detector is used to provide an input to the trigger system, which can control the acquisition process. The resultant time-domain record is stored in memory.
Data is then read from memory by the Digital Downconverter (DDC), which essentially band limits the signal to a range of frequencies corresponding to the current span and center frequency settings. The resultant data is then fed to the DSP/ Display system for further processing and display.
The elements of this block diagram will be discussed in more detail in the following sections.
Block Downconversion
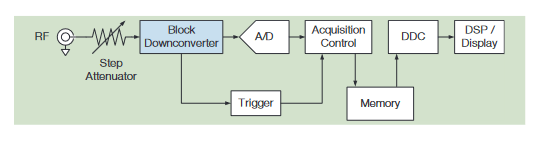
Because of the oscilloscope-based acquisition system in the MDO4000C, a straightforward block downconverter is used to bring the frequency span of interest into the range of the A/D converter.
The block downconverter is switched between the ranges shown in Figure 33.
Notice that the three frequency bands overlap by 1 GHz. This allows the MDO4000C to provide a minimum of 1 GHz of single-shot capture bandwidth at any center frequency setting. This greatly exceeds the 10 MHz capture bandwidth of the typical modern spectrum analyzer. It also excels when compared to the (very expensive) options to extend the capture bandwidth to 40, 80, or even 160 MHz in these analyzers.
Also note that quite often the capture bandwidth will exceed this 1 GHz minimum. Indeed, in the 3.0 GHz MDO4000C, the instrument is always capturing the spectrum in a single acquisition, at any span setting.
When the displayed span exceeds the limits of one downconverter band, two bands can be stitched together seamlessly to build a spectrum from two records.
RF Domain Triggering
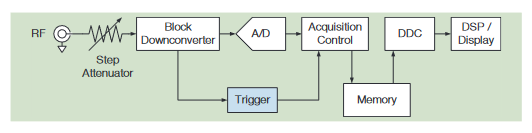
The oscilloscope-based acquisition system in the MDO4000C also provides an inherently triggered acquisition system. Data is acquired in a single contiguous time-domain record. This record is then digitally downconverted to the desired span and then run through a DFT to convert it to the frequency domain. As a result, the entire set of frequency-domain data displayed for a single acquisition is time consistent – it comes from the same triggered data record.
This process is in contrast to the typical gated sweep in a conventional spectrum analyzer. A gate signal can “trigger” the sweep, but the signal being viewed can still change during the sweep time. The result is little certainty that the displayed frequency information is time consistent. With more sophisticated time gating, a spectrum can be builtup over time from multiple trigger events, but the result still does not represent data from a single contiguous time period which is often times crucial for diagnosing intermittent bugs in embedded systems. This technique can only work with repetitive events.
The MDO4000C also provides a free-run option for spectrum displays, to avoid displaying a spectrum that is synchronized to some event in the DUT. This mode is still “triggered” in that the displayed spectrum is still extracted from a contiguous data record and, therefore, time consistent. The difference is that the trigger events are internally generated, as fast as possible, to avoid correlation with events in the DUT.
Acquiring the Raw RF Time Domain Data Record

In order to understand the process of acquiring time-domain data to convert to the frequency domain, a brief discussion of the relationships between data in these two domains is necessary.
First, the amount of time sampled to create a single spectrum is driven by the RBW setting and the Window choice. This acquisition time is called the Spectrum Time. Simplistically (ignoring the Window term), the formula for acquisition time is as follows:
Spectrum Time > 1 / RBW
The RBW setting represents the smallest frequency difference that can be discerned in the frequency axis. Setting the RBW to, for instance, 1 Hz, requires that greater than 1 second (1/1Hz) of data be acquired for analysis. This is simple to understand if one notes that it will take 1 second to tell the difference between a 1000 Hz and a 999 Hz signal. It takes this long to “count” the full 1000 cycles in the first signal and the 999 cycles in the second signal. Differences below 1 Hz cannot be discerned over this time interval.

The Window function (see Generating the Spectrum for more information on the window function) has an inherent filter shape that affects the bandwidth of the FFT conversion process, smearing energy into adjacent bins. The Window Factor specifies the -3dB bandwidth of the window, in number of FFT bins. The impact of the window factor is to extend the required acquisition time by the window factor as follows:
Spectrum Time = Window Factor x (1 / RBW)
The window factors for the various FFT windows found in the MDO4000C are shown in Table 4 along with the respective Spectrum Time.
Second, the minimum sample rate is driven by the Span and Center Frequency settings. The Nyquist Theorem specifies that the sample rate must be a minimum of twice the highest frequency component found within a digitized signal. If the sample rate is insufficient, aliasing will occur, resulting in false indications of signals at frequencies that are not present in the signal.
In order to avoid this aliasing, the input signal must be lowpass filtered above the highest frequency of interest. This is illustrated in Figure 34.
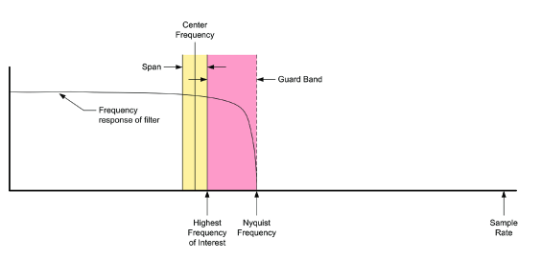
As a result, the required minimum sample rate is defined as follows:
Sample Rate = 2 x Filter Factor x (Center Frequency + ½ x Span)
The filter factor (FF) is a term that is relative to the highest frequency of interest, and defines a guard band that ensures that the signal is attenuated below the SFDR of the instrument at the Nyquist frequency.
Unlike many new Vector Signal Analyzers, the MDO4000C does not need to provide variable input filtering or adjust the acquisition sample rate, since the A/D converter samples at a constant 10 GS/s rate. This is high enough to provide the 3.75 GHz of input bandwidth necessary for the block downconverter.
Sampling at fast sample rates provides digital processing gain when considering the noise power of signals within a given span. Processing gain reduces noise power by 10 log of the ratio of Nyquist bandwidth divided by the resolution bandwidth.
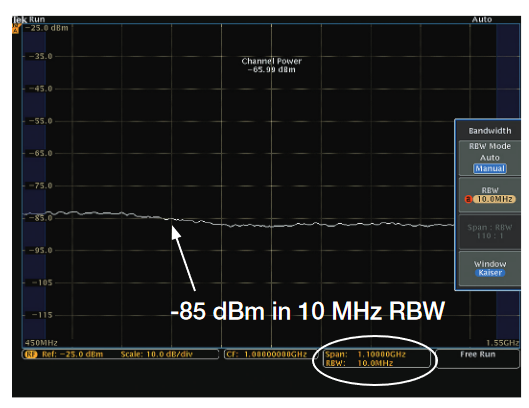
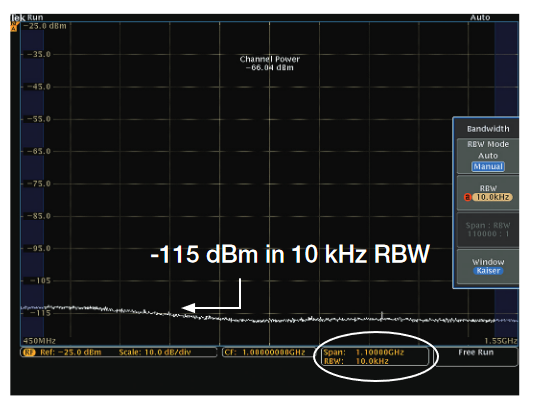
As an example, the noise power of a 1 GHz channel as shown in Figure 35 has been measured as -65.99 dBm. The noise power must be considered as a component of measurement uncertainty when measuring a signal of interest. In theory, the process gain at a constant sample rate over a fixed bandwidth can be demonstrated by reducing the resolution bandwidth. The noise floor across the 1 GHz span in Figure 35 at a 10 MHz RBW is approximately -85 dBm. In Figure 36, we now reduce the RBW in the same span 3 orders of magnitude to 10 KHz RBW. While the noise power across the span remains constant (now -64.04 dBm), the noise floor across the 1 GHz span is now down at -115 dBm. This is a 30 dB improvement to the noise floor while the overall noise power of the channel power has remained constant.
Unlike a traditional oscilloscope, being able to select a span of interest at a specific frequency can also reduce the noise power in the measurement, thus reducing uncertainty when measuring low level signals.
Finally, the acquired data record for the spectrum analyzer channel is defined as the maximum RF Acquisition Time. RF Acquisition time is a function of the sample rate and the memory size. Since the sample rate is fixed at 10 GS/s, and there is 1 GB of memory in the spectrum analyzer path, in theory one should be able to achieve 100 ms of time from the spectrum analyzer input. However, in addition to storing the sampled RF data, memory is also used to compute the RF versus time for acquisition, the downconverted RF I & Q data, the waveform raster display, sin/cos mixing tables, and RF traces. This includes amplitude, frequency, and phase versus time calculations and complex IQ data. At wider spans, there is less decimation (data compression) for these time-domain records, so this impacts the amount of time available for RF acquisitions.
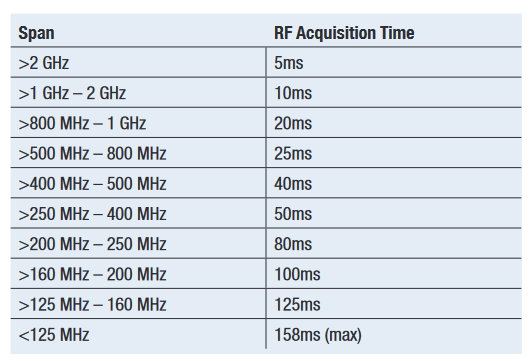
Table 5 has the RF Acquisition Time versus Span available in the MDO4000C. The narrow spans with substantial decimation can achieve the longest time records. As instantaneous bandwidths increase, the amount of data allocated to RF Time Domain traces begins to dominate the memory allocations.
RF Acquisition time is at least as long as Spectrum Time and in most cases will be much longer. It is also important to know that Spectrum Time can be panned through the RF Acquisition time and FFTs will be recalculated and displayed in the Frequency Domain view.
Another important variable to consider is the Analog Time. Analog Time is the amount of time acquired by the analog and digital channels and is directly controlled by the horizontal scale knob. Since the amount of time that is acquired on the analog and digital channels is completely independent of the spectrum analyzer, it is important to understand how these two functions relate to each other.
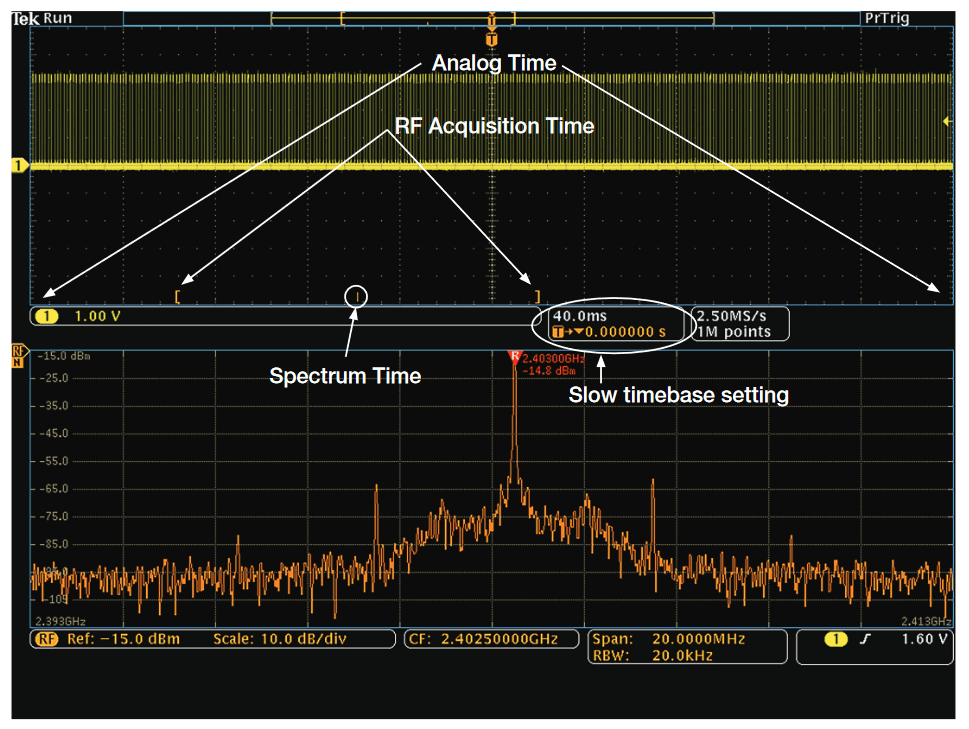
For mid-to-fast timebase settings, RF Acquisition Time and Analog Time are equivalent and the user can move Spectrum Time across the entire acquisition. However, when slower timebase settings are used, and the effective sample rate of the analog channels is reduced, Analog Time can exceed RF Acquisition Time. In these cases, it is important for the user to understand what portion of the Analog Time represents the RF Acquisition time. Figure 37 shows the relationship for the Analog Time, RF Acquisition Time, and Spectrum Time for a very slow timebase setting in the Time Domain View.
It is important to understand that an RF Acquisition must have a trigger event to correlate the Frequency and Time Domain view. The trigger event can occur at the end of an RF Acquisition, as shown in Figure 37, or the RF Acquisition can occur at any time after the trigger.
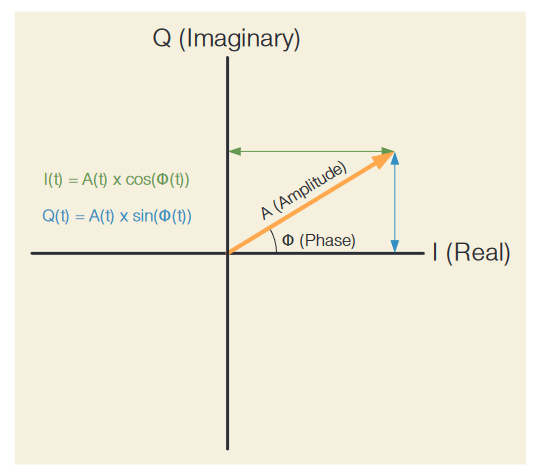
Digital Downconversion
A common and computationally efficient way to represent bandpass signals is to use the complex baseband representation of the waveform. The first step in converting to the frequency domain is to perform Digital Downconversion on the raw RF time-domain record. This process achieves three things:
- The data record is converted to a complex I (in-phase) and Q (quadrature) data format
- The center frequency is moved to DC, to allow the IQ sample rate to be reduced to half rate
- The data is filtered and decimated to a sample rate sufficient to cover the span
To generate IQ data, and move the center frequency (CF) to DC, the raw RF time domain data is multiplied by sine and cosine terms as follows:
I = RF(t) x cos(CF)
Q = RF(t) x sin(CF)
The resultant IQ data is complex, and represents how the RF signal deviates from the center frequency over time. This is illustrated in Figure 38.
The downconverted signal, at any point in time, can be viewed as a vector drawn in the IQ plane. The instantaneous amplitude of the signal establishes the length of the vector. The instantaneous phase of the signal, with respect to the center frequency, establishes the polar angle of the vector. The I and Q values are the projections of this vector onto the I (real) and Q (imaginary) axes.
It is critical to understand that the phase of the signal is relative to the current center frequency setting. To understand more fully, consider the following:
- If the input is a Continuous Wave, CW, signal at exactly the same frequency as the center frequency setting, the resultant vector will be stationary in the IQ plane. The phase of the vector is just the phase offset between the signal and the center frequency.
- If the input signal is an amplitude modulated CW signal at exactly the same frequency as the center frequency setting, the resultant vector will again have a constant phase angle, but will vary in length as the amplitude changes.
- If the input signal is a CW signal at a different frequency from the center frequency setting, the resultant vector will rotate around the center of the IQ plane at a rate that represents the difference in frequency between the CW signal and the center frequency.
Once this conversion to IQ data has taken place, the span of interest is centered at DC. The IQ data can then be filtered to remove any frequency components outside of the span and decimated to reduce the data content. Similar to the sampling described previously, the desired span setting determines the minimum resultant sample rate:
Minimum Sample Rate = 2 x Filter Factor x (½ x Span)

Since the center frequency is now zero, it cancels from the equation. The sample rate need only be based on ½ of the span, since complex IQ data is twice as efficient at carrying frequency information as real data. With IQ data, the Nyquist frequency is equal to the sample rate.
n the MDO4000C, the filter factor is typically about 1.5.
This downconversion process is illustrated in Figure 39.
Generating the Spectrum
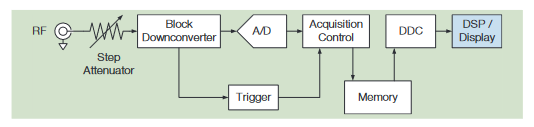
Figure 40 illustrates the process of generating the spectrum trace for display.
The first step in the process is to multiply the data by the window function. Since the FFT assumes that the signal is unchanging throughout time, discontinuities at the ends of the sample interval will show up as spectral leakage in the resultant spectrum. The window function reduces these discontinuities. For more information on the various window functions and their usage, see Appendix A: Windowing Functions.
One implication of the assumption that the signal is unchanging through time is that a signal that changes amplitude during the time interval covered by the RF timedomain data will show up in the resulting spectrum with a diminished power level. The only way to avoid this is to adjust the RBW setting to ensure that the signal is stable throughout this time interval.
Since FFT processing is more efficient with power of two data lengths, the input data is zero padded up to the nearest power of two. The zero padding adds spectral resolution without changing the frequency content.
It is interesting to note that the length of FFT used is entirely dependent on the Span/RBW ratio. It can easily be shown from the formulas above, that:
FFT Length = (Window Factor * Filter Factor * (Span)) / RBW
For the MDO4000C, the window factor for the default Kaiser window is 2.23. As noted above, the filter factor is roughly 1.5. The default span / RBW ratio is 1000:1. With these default settings, the resultant FFT length is approximately 3,345 points. This is zero-padded up to a 4,096 point FFT.
The greater the number of samples in the spectrum time, the finer the frequency resolution after the transformation is complete. Unfortunately, this also means the greater the number of necessary data computations, to transform the data. The FFT process is well-known for its intense computational requirements.
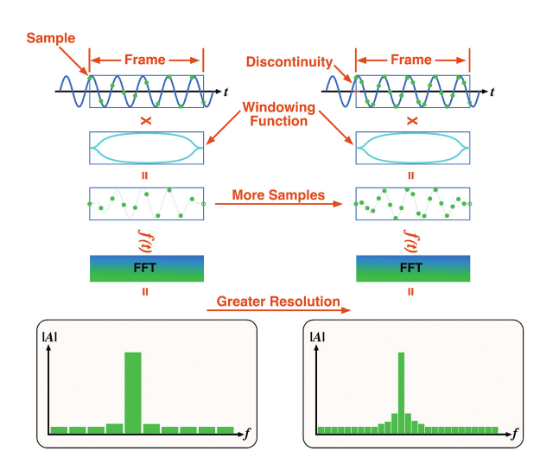
An FFT is then used to convert the RF time-domain data to frequency-domain data, in the form of a spectrum. This spectrum is then modified further:
- The entire spectrum is multiplied by a set of coefficients that adjust the flatness and phase. These coefficients are determined during factory calibration.
- As previously discussed, the FFT process can involve between 1,000 and 2,000,000 points. As a result, the spectrum record may be decimated to fit the 1,000 point display. This decimation process is called Detection, and is used to aggregate multiple FFT bins into a single display bin. The user has control over the detection selected and the decimation behaves as follows:
- + Peak: Keep the largest data point in the decimation interval
- – Peak: Keep the smallest data point in the decimation interval
- Average: Average the data throughout the decimation interval
- Sample: Keep the first data point in the decimation interval
- The resulting spectrum is then log scaled for final display.
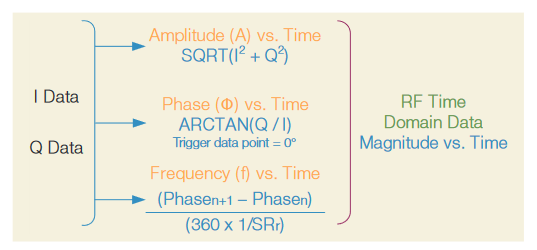
Generating RF Time Domain Data
Another use for the IQ data is in generating RF Time Domain Data. Recall, from Digital Downconversion, that the IQ data is merely a Cartesian representation of the signal plotted as a vector in the imaginary IQ data plane. As such, the IQ data can be transformed as shown in Figure 42.
The resulting RF time-domain data can be plotted, along with other time-domain traces, in the time-domain graticule. All time-domain data, including the analog, digital, and spectrum analyzer channels are time-aligned in the graticule, allowing the user to evaluate timing relationships between these various channels.
Notice that the phase and frequency calculations are both made independent of the amplitude calculation. If the amplitude is low, the IQ data becomes increasingly dominated by noise. This effect is shown in Figure 43.
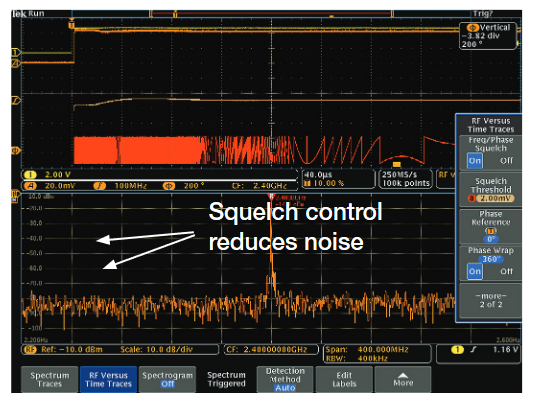
In order to avoid this problem, the MDO4000C has a squelch control that allows the user to blank the phase and frequency traces when the amplitude falls below a user-defined threshold. The result is shown in Figure 44.
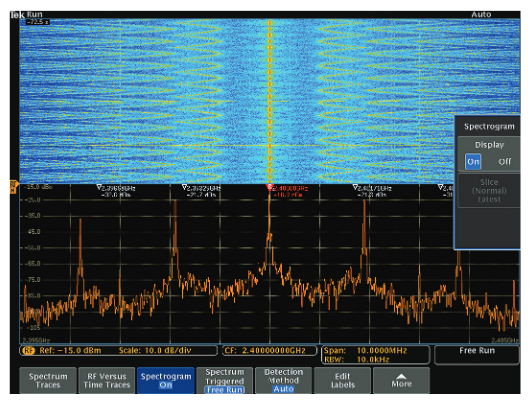
Generating the Spectrogram
Another use for the spectrum is in plotting the spectrogram.
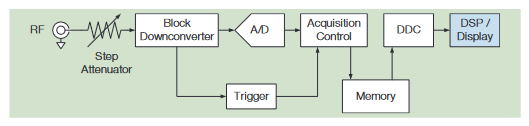
This is a relatively simple process of encoding the magnitude of the spectrum in color and drawing the result as a single line of pixels in the spectrogram display. Each new “slice” pushes the existing data up in the display until it is discarded at the top of the display. A “slice” is representative of a single FFT that has been process based on the Span and RBW settings in the Spectrum Display

Time Resolution
One final topic worth discussing is the time resolution of the data.
The spectrum has relatively poor time resolution. The reasons for this can be seen in Figure 47.
First, as noted previously in Generating the Spectrum, the FFT is generated from data covering a time interval defined by the RBW setting. Changes in the spectral content of the signal within this time interval cannot be discerned – they are aggregated into a single spectrum.
Second, as seen in Figure 47, there is a delay between acquisition events. Changes that occur between acquisition events will not be visible.
To reduce the time over which the spectrum is calculated, the RBW should be increased. With the default setting that links RBW to span, increasing the span will have the desired
effect. This has the additional effect of reducing the time between acquisitions, since the time required to do the digital downconversion is reduced.
To further reduce the time between acquisitions, the span/ RBW ratio should be lowered. This results in a faster FFT processing time.
In comparison to the spectrum, the RF time-domain data has relatively good time resolution. As noted in Digital Downconversion, the sample rate of the IQ data is driven by the span setting and, as such, is much finer than the spectrum time resolution. This is one of the main advantages of the RF time-domain traces.
To improve the time resolution of the amplitude, phase, or frequency vs. time traces, the span should be increased.
Appendix A: Windowing Functions
Windowing
There is an assumption inherent in the mathematics of Discrete Fourier Transform (DFT) analysis that the data to be processed is a single period of a periodically repeating signal.

Figure A1 depicts a series of time-domain samples. When DFT processing is applied to Frame 2 in Figure A1, for example, the periodic extension is made to the signal. The discontinuities between successive frames will generally occur as shown in Figure A2.
These artificial discontinuities generate spectral artifacts not present in the original signal. This effect produces an inaccurate representation of the signal and is called spectral leakage. Spectral leakage not only creates signals in the output that were not present in the input, but also reduces the ability to observe small signals in the presence of nearby large ones.
The MDO4000C Series Spectrum Analyzer function applies a windowing technique to reduce the effects of spectral leakage. Before performing the DFT, the DFT frame is multiplied by a window function with the same length sample by sample. The window functions usually have a bell shape, reducing or eliminating the discontinuities at the ends of the DFT frame.
The choice of window function depends on its frequency response characteristics such as side-lobe level, equivalent noise bandwidth, and amplitude error. The window shape also determines the effective RBW filter.
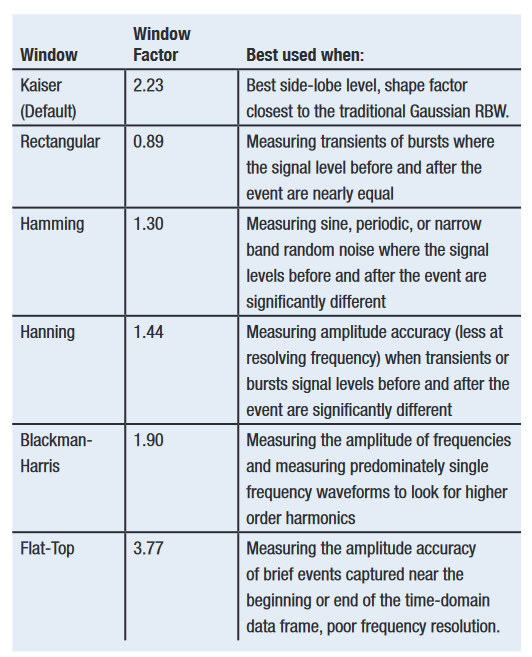
Like other spectrum analyzers, the MDO allows the user to select the RBW filter. The MDO also allow the user to select among many common window types. The added flexibility to directly specify the window shape enables the users to optimize for specific measurements. Special attention, for example, should be paid to the spectrum analysis of pulse or transient RF signals. Table A1 gives some suggestions on the use of different window functions.
The magnitude of the frequency response of the window function determines the RBW shape. For example, the RBW on MDO is defined as the 3 dB bandwidth and is related to the sampling frequency and samples in the DFT as follows:
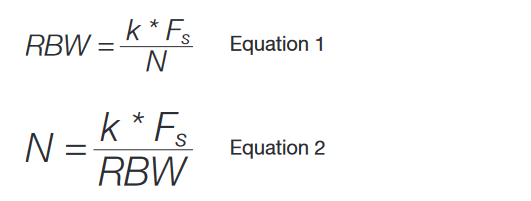
Where k is a window-related coefficient, N is the number of time-domain samples used in the DFT calculation, and Fs is the sampling frequency. For the Kaiser window the value of k is about 2.23. The RBW shape factor, defined as the frequency ratio between the spectrum amplitude at 60 dB and 3 dB, is about 4:1. On the MDO, the spectrum analysis measurement uses Equation 2 to calculate the required number of samples for the DFT based on the input span and RBW settings.
The time domain and the spectrum of the Kaiser window used for MDO spectrum analysis is shown in Figure A3 and Figure A4. This is the default window used in the MDO4000C for spectrum analysis.
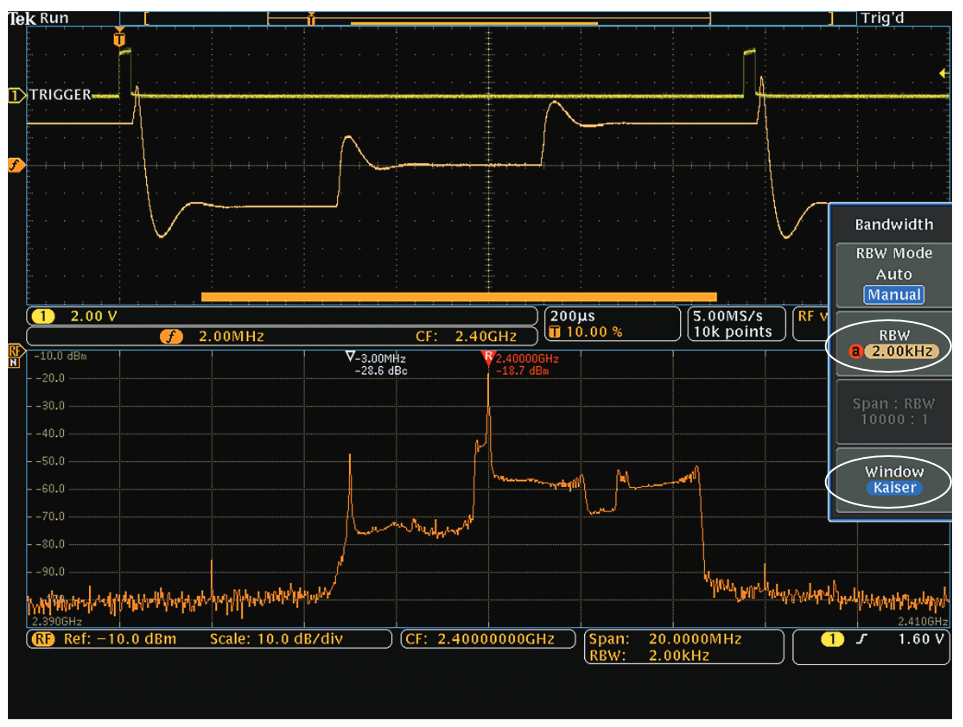
An example of how different windows impact the spectrum representation of a time-varying signal, consider the frequency-hopping signal in Figure A5. Using the default Kaiser window, the Spectrum Time associated with this acquisition is 1.12 ms. The frequency versus time display shows that the Spectrum Time is roughly centered for most of the hop on the middle frequency of the triple hop sequence. While there are roughly equivalent times associated with the “on-frequency” period of the lower and upper frequencies,the window function described in Figure A3 shows that the time samples near the beginning and edge of the acquisition are reduced in level, as a Gaussian distribution of samples in the center of the acquisition is used in the windowing function. Looking at the amplitude of the four peaks in the Frequency Domain display (center frequency, high frequency, low frequency, and maximum overshoot peak), the center peak is nearly 30 dB above the other signals.
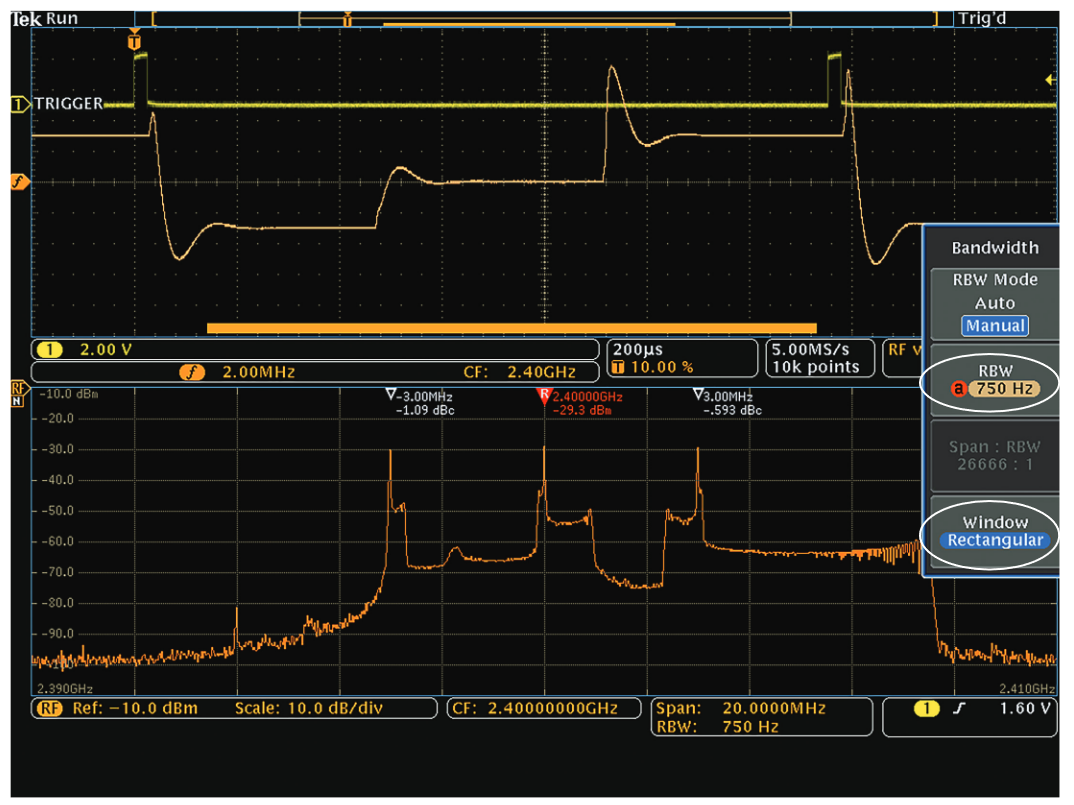
In Figure A6, the Window type is now selected to be Rectangular. Since the Window function of the Rectangular Window is different that the Kaiser Window, the RBW has been changed to 750 Hz so the Spectrum Time becomes roughly equivalent to the acquisition time in the previous example shown in Figure A5.
Again, the Spectrum Time is aligned to roughly the same point in the triple hop sequence; however the spectrum representation is substantially different.
Since the Rectangular Window function essentially does not filter the time samples across the acquisition time, and the dwell time on each of the three frequencies is roughly
equivalent, the spectrum using the Rectangular Window shows a spectrum of three peak signals at roughly the same amplitude.
Other windows (such as Blackman-Harris, Rectangular, Hanning) may be user-selected to meet special measurement requirements, and may be used by the instrument when performing some of the measurements available in the instrument.


